基于Matlab电动车机器人系统辨识与仿真
型号: PXF0172
模型就是把关于实际系统的本质的部分信息简缩成有用的描述形式,它的主要功能是模拟实际系统的行为,而不是去描述实际系统的实际结构。模型可以分为物理模型和数学模型。建立数学模型一般有机理建模、黑箱建模和灰箱建模三种方法。
1.1 机理建模
又称理论建模或白箱建模,根据所研究系统的物理机理,利用物质和能量的守恒性以及连续性原理、有关物理定律(牛顿定理、流体力学、热力学定律等),考虑物理量之间的关系,推导出数学模型。此方法适用于简单系统的建模,通常能达到精度要求。
1.2 系统辨识
又称试验建模或黑箱建模,对于一个已存在的实际系统,根据观察,测量并记录得到的输入输出数据,经过一些加工处理,求出非参数或参数模型,这种建模方法就是系统辨识。这种方法不需要深入了解过程的机理,需要的先验知识少,能提供由其他方法难以建立的环境或噪声的动态特性。
1.3 机理建模和辨识相结合的建模法
又称灰箱建模,对系统进行数学建模时,机理已知的部分采用理论建模方法,机理未知的部分采用辨识建模的方法,发挥两种方法各自的优点,建立更为精确的数学模型。
系统辨识是控制论的一个分支,系统辨识、状态估计、控制理论构成了现代控制论的三大支柱。随着各门学科的定量化,系统辨识的应用越来越广泛,不仅是航空、航天、电力、化工等工程应用领域,还延伸到生物信息学、医学工程、社会经济等多各学科。以下是不同时期的学者给系统辨识下的定义。
系统辨识(System Identification)就是在输入和输出数据的基础上,从一组给定的模型类中,确定一个与所测系统等价的模型。属于黑箱模型。
辨识问题可以归结为用某个模型来辨识客观系统(或将要构造的系统)本质特征的演算,并用这个模型把对客观系统的理解表示成有用的形式。
辨识有3个要素——数据、模型类和准则。辨识就是按照某个准则在模型类中选择与数据拟合最好的模型。其中,数据(能观测到的输入或输出数据)是辨识的基础,模型类(所考虑的模型的结构)是寻找的模型范围,等价准则(用来衡量模型接近实际系统的标准)是辨识的优化目标。
总而言之,系统辨识的实质就是按照某种原则,利用所观测到的含有噪声的输入输出数据,从一类模型中确定一个与所测系统拟合最好的模型。
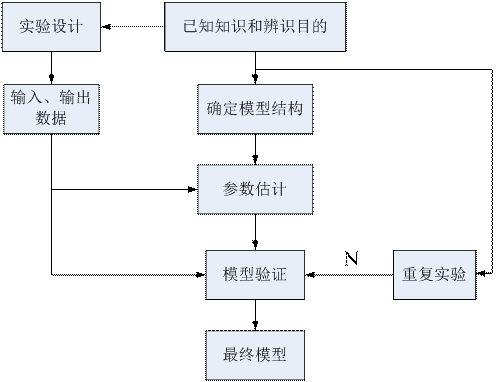
图3-1 系统辨识的内容及步骤
3.1 获取验前知识、明确辨识目的
在辨识之前应了解尽可能多的有关对象的知识,以减少辨识过程中的困难。需要知道辨识的一般过程、系统运行条件、工作过程、支配过程的物理定律、某些预测试验。
获取预备知识的首要问题是辨识目的,欲了解系统的某些特性(自然频率、阻尼系数、放大系数等),只要非参数模型(如波德图)即可;欲对系统进行控制(如自适应控制),则需找出参数模型。辨识的目的将决定模型类型、精度要求、辨识要求、辨识方法。
3.2 实验设计
安排实验的目的是为了获得输入输出数据。输入变量应能够设置,且必须包含足够丰富的频率分量,输出变量应能够测量,并且和我们感兴趣的现象有关。设计实验的原则是所获得的数据(对研究目的来说)包含的信息要尽可能地多。当然,还要考虑到实现的可能性及实验费用等。
实验设计中要考虑的问题包括:在系统输入允许的情况下,如何选择输入信号、采样速度、实验期限及做哪些预备性实验等。由于观测到的数据一般含有噪声,因此辨识建模实际上是一种试验统计方法。
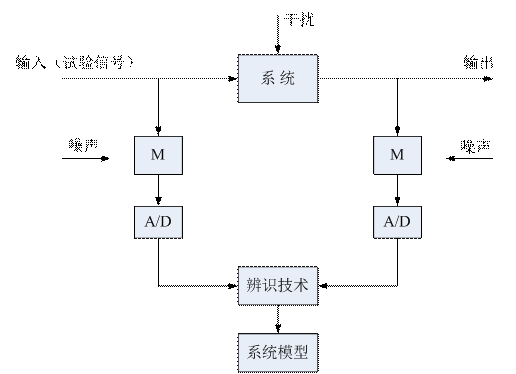
图3-2 实验设计
3.3 确定模型结构
除了单变量线性系统的阶、多变量线性系统的结构不变量和一些逼近算法的近似模型,模型的结构主要是依靠先验知识来决定的。模型形式有多种,最常见的是随机、线性、动态、离散系统。在这一环节中,要注意模型阶次的选择、纯滞后时间的估计等方面。
3.4 参数估计
模型的未知部分是以未知参数的形式出现的。我们需要通过某种方法确定未知参数,从而得到参数模型。模型结构确定后,辨识主要就是通过实验数据去估计未知参数。因此,参数估计是辨识工作的主要内容,是一个具体的辨识过程中工作量最大的部分。
3.5 模型验证
将实际的测量输出和模型的计算输出相比较,模型参数应当保证两个输出之间在选定意义上的接近。若不一致,需修改模型结构的假设,修改实验设计,重复试验。解决这个问题目前还没有什么系统的方法,只是随着问题的不同而提出具体的解决办法。
借助MATLAB系统辨识工具箱(如图4-1所示)进行建模,可简化计算过程、提高效率,使建模过程直观、形象。利用MATLAB系统辨识工具箱进行系统辨识主要包括以下内容:观测数据的获取、数据预处理、模型结构的选择、参数估计、模型检验与动态仿真。
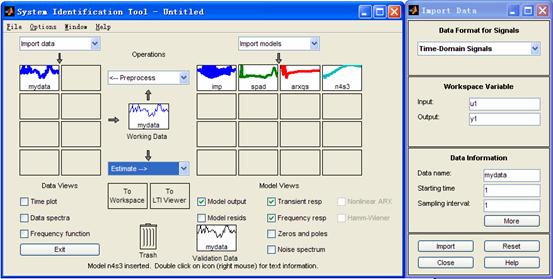
图4-1 系统辨识工具箱
4.1 观测数据的获取
观测数据含输入、输出、噪声等,工具箱提供系统辨识的输入信号函数idinput,调用格式为:u=idinput(N,type,band,levels)。函数idfilt利用Butterworth滤波器对数据进行滤波,利用idresamp函数对输入输出数据进行重新采样来插值或删减数据等。
4.2 数据预处理
系统建模时,要求输入输出数据的统计特性与统计时间起点无关,且均值为0。而实际测量直接得到的数据是随机时间序列,为了获得更符合实际情况的系统模型,必须先对测量数据进行预处理。主要包括消除数据的趋势项、对测量数据进行滤波和重新采样。在系统辨识工具箱中,函数dtrend用来去除输入输出数据中的趋势项,调用格式为:zd=dtrend(z,o,brkp)。
4.3 模型结构的选择
系统辨识工具箱提供对多种模型类的支持,包括非参数和参数等模型类。非参数模型类包括脉冲响应和频域描述等模型。参数模型类有ARX、ARMAX、BJ、输出误差和状态空间等模型。
系统辨识工具箱提供的模型结构选择函数有struc、arxstruc、ivstruc和selstruc。
在此次电动车机器人系统辨识课题中,我们选用ARX模型来实现系统辨识。这就意味着我们将假定系统的真实模型具有ARX模型的结构。其结构如下:
A(z-1)Y(k)=B(z-1)U(k)+e(k)
通过寻找一个具有较小AIC值的估计模型来决定模型的阶次。AIC值由下式定义:
AIC=Log(V)+2d/N
式中,V为损失函数,d为估计参数的个数,N为估计数据的个数。
4.4 参数估计
系统辨识工具箱中,支持的参数模型包括AR、ARX、ARMAX、BJ、状态空间和输出误差等模型,含一次完成和递推辨识等算法。一次完成算法的参数模型辨识函数有ar、arx、armax、ivx等。用递推算法进行参数模型辨识的函数有rarx、rarmax等。
4.5 模型检验与动态仿真
工具箱中,用于模型验证和仿真的函数主要有compare、resid、pe、predict和idsim。其中:compare可将模型的预测输出与对象实际输出进行比较,resid用来计算和检验模型残差;pe计算预测误差;predict预测未来输出;idsim可进行模型仿真计算。
本次设计中,我们选择参数模型类ARX进行建模,利用struc函数生成多个模型结构参数,利用arxstruc函数计算多个单ARX模型的损失函数,而selstruc函数用于确定阶次和选择模型结构,arx函数可以计算出ARX模型参数。
5.1 观测数据的获取
在电动车机器人系统辨识问题中,用来完成系统辨识的数据为一组单输入单输出数据,即SISO数据,由两部分构成:作为输入数据的电动车机器人把手驱动电机的驱动电压(单位为毫伏)和作为输出数据的电动车机器人车体相对垂直方向的倾斜角度(单位为度)。驱动电压u通过电位计测量而来,倾斜角度y通过倾角传感器测量所得。这些数据属于随机时间序列,包含有线型或缓慢变化的趋势。本次设计我们得到两组数据,一组用于建模,另一组用于模型验证。
5.2 数据预处理
系统参数设定:输入u(k)为电压,输出y(k)为传感器测量得到的电动车机器人车体倾斜角度。bicycle2.mat为系统输入/输出的测试数据。系统模型结构如图5-1所示。

图5-1系统模型结构图
y1包含150个倾角测量值,u1为150个输入电压采样值,采样周期为1/15s。首先我们将系统输入/输出数据设置成IDDATA对象形式:
load bicycle1
datal=[1653 -8 1656 -5 1656 -3 1656 -2 6565……1955 -5 2001 -4]; %导入所有150对测量数据
u1=data1(1:2:299); %生成150个输入数据组成的输入向量
y1=data1(2:2:300); %生成150个输出数据组成的输出向量
ul=ul’;
yl=yl’; %将输入输出向量转化为列向量,以满足iddata函数格式要求
bicycle1=iddata(y1,u1,1/15); %生成包含输入输出数据的iddata对象
bicycle1.inputname=‘驱动电压’;
bicyele1.outputname=‘车体倾角’;
ze1=bicycle1(1:75); %取其中的75对数据作为模型辨识的输入、输出数据向量
figure,plot(ze1(1:75)) %绘制其中75对数据的输入输出图象
运行结果如图5-2所示。
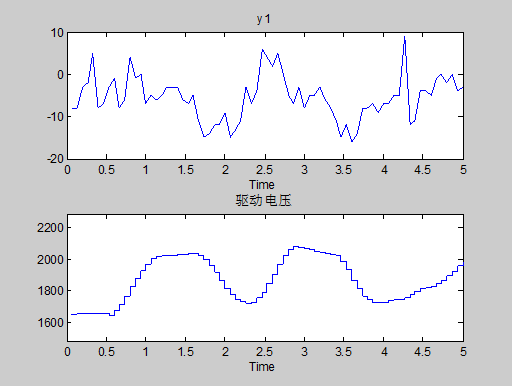
图5-2 输入输出图像
从图象可以明显看出,该序列的均值不为零,而且随时间变化,因此必须进行平稳化预处理,主要是消除数据的趋势项,把测量的数据变成均值为零的平稳过程。在此我们采用MATLAB系统辨识工具箱中的dtrend函数。
zel=dtrend(zel); %对用于辨识的输入、输出数据向量进行数据预处理;
运行结果如图5-3所示。

图5-3 数据预处理结果
从图中可以看到,经过数据预处理后的测量数据消除了数据中的趋势项,获得了比较理想的处理效果。
5.3 模型结构的选择和阶次确定
我们选择参数模型类ARX进行建模,调用格式为:M=ARX(DATA,ORDERS)。其中,ORDERS=[na nb nk],为模型阶次向量;DATA为辨识模型的输入输出数据组。ORDERS的值取一定范围内(na、nb、nc的变化范围均为1到10)估计模型的AIC值最小的模型所对应的阶次。
MATLAB中模型结构选择函数为selstruc,AIC极小化模型选择函数的调用格式为:nn=selstruc(V,’aic’),其中,V为各个模型结构的损失函数。故为求得模型的阶次必须得到各个模型结构的损失函数。
MATLAB中计算多个单ARX模型损失函数的函数为arxstruc,调用格式为:V=arxstruc(ze,zv,NN)。其中,ze为用于模型辨识的输入、输出数据向量或矩阵;zv为用于模型验证的输入、输出数据向量或矩阵;NN为多个模型结构参数构成的矩阵,NN每一行具有如下形式:nn=[na nb nk]。
而生成多个模型结构参数的函数为struc,调用格式为NN=struc(NA NB NK),其中NA、NB、NK分别为ARX模型多项式A(q)、B(q)的阶次范围和纯时延大小范围。
用于模型结构选择和阶次确定的代码如下:
NN=struc(l:10,l:10,l:10); %生成多个模型结构参数
V=arxstruc(bicycle1(1:75),bicycle1(75:150),NN); %计算多个单ARX模型的损失函数
nn=selstruc(V,’aic’); %确定阶次,选择模型结构
经编程求得最佳模型阶次组合为(2,1,4)。
5.4 确定模型参数![]()
MATLAB中提供了多种参数辨识的方法和函数,我们选取其中的基于最小二乘法估计的ARX参数辨识方法,即调用ARX函数进行模型参数确定。
M=arx(zel,[2,1,4]); %确定ARX模型参数
运行后得到的模型参数为:
Discrete-time IDPOLY model: A(q)y(t) = B(q)u(t) + e(t)
A(q) = 1 - 0.3683 q^-1 - 0.08285 q^-2
B(q) = -0.01239 q^-4
Estimated using ARX from data set ze1
Loss function 15.7651 and FPE 17.0789
Sampling interval: 0.0666667
5.5 模型阶数验证和模型验证
为了验证ARX模型的有效性,另采样提取了一组数据(去除趋势项后,如图5-4所示),比较了模型输出与系统实际输出(图5-5),并进行了相关性分析(图5-6)。结果显示:模型输出和系统实际输出之间存在一定的误差,相关性和互相关性表明,所建模型的模型输出基本上能够拟合系统实际输出,描述系统在固定平衡点的动态特性。

图5-4 去趋势项后的输入输出图

图5-5 模型输出与测量输出比较图
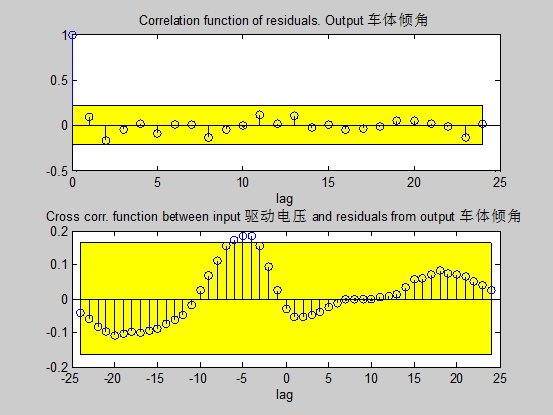
图5-6 模型误差相关分析图
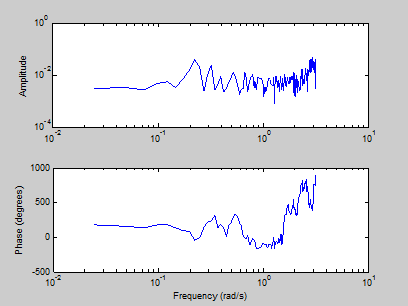
图5-7 频率响应图
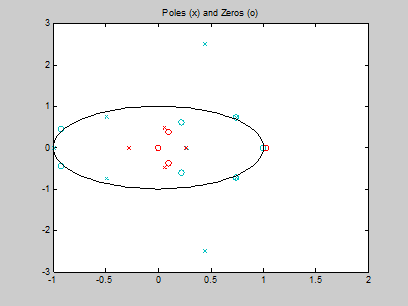
图5-8 零极点分布图
本文对电动车机器人控制系统进行了ARX建模研究。首先,选用AIC准则作为系统模型阶次的选择原则选定了系统模型的阶次;然后以最小二乘法来辨识模型的全部参数,建立了电动车机器人控制系统的ARX模型;最后,另采样获取一组数据,对模型的有效性进行了验证,从模型的预测输出和系统实际输出的拟合效果来看,该模型的有效性能够达到要求。
应用ARX建立的系统模型为线型模型,在一定程度上能够反映实际系统,用这种方法建立模型的过程所需时间短,响应快速;缺点是模型精度不够高。而基于Matlab神经网络建模得到的模型(非线性模型)精度较高,但响应的时间远大于基于ARX模型的系统辨识,图6-1是利用神经网络中的BP算法逼近函数y=2cos(2x)+2exp(x),可见逼近效果非常理想,由于篇幅有限,这里不再做过多的讨论。
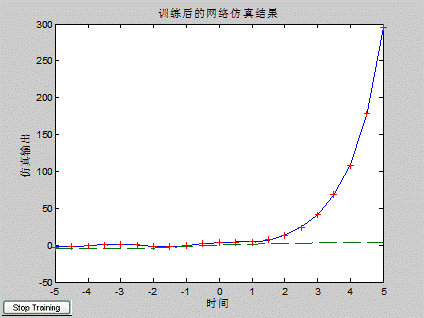
图6-1 利用BP算法逼近函数y=2cos(2x)+2exp(x)
通过对系统辨识一些简要模型的设计与仿真,我加深了对系统辨识相关知识的理解,从中学到了很多建模与辨识的知识,初步掌握了系统辨识工具箱的使用方法,对Matlab编程语言有了进一步的认识,编程能力也有所提高。在这次设计中由于缺少真实的实际系统,设计与仿真的结果还存在一些缺陷,还望老师给予批评和指正。最后感谢任老师一个学期来的悉心指导,感谢程贝贝学姐对我的无私帮助,感谢西安交大李伟同学、西安电子科大严鹏涛同学、成都电子科大储童松同学提供的宝贵资料。
[1] 刘宏才.系统辨识与参数估计[M],北京:冶金工业出版社,1994
[2] 齐晓慧,田庆民,董海瑞.基于Matlab系统辨识工具箱的系统建模.兵工自动化[J],2006,Vol25,No.10
[3] 潘立登,潘仰东.系统辨识与建模[M],北京:化学工业出版社,2004
[4] 王秀峰,卢桂章.系统建模与辨识[M],北京:电子工业出版社,2004
data1=[1653 -8 1656 -8 1656 -3 1656 -2 1656 5 1656 -8 1656 -7 1646 -3 1675 -1 1714 -8 1769 -6 1827 4 1875 -1 1930 0 1972 -7 2004 -5 2014 -6 2020 -5 2020 -3 2020 -3 2027 -3 2036 -6 2039 -7 2039 -5 2020 -11 2001 -15 1962 -14 1917 -12 1865 -12 1814 -9 1778 -15 1743 -13 1733 -11 1720 -3 1730 -7 1756 -4 1791 6 1846 4 1904 2 1969 5 2023 0 2065 -5 2078 -7 2075 -3 2068 -8 2062 -5 2052 -5 2043 -3 2039 -6 2030 -8 2020 -11 1988 -15 1933 -12 1869 -16 1817 -14 1769 -8 1746 -8 1727 -7 1727 -9 1730 -7 1740 -7 1743 -5 1746 -5 1759 9 1782 -12 1798 -11 1814 -4 1820 -4 1827 -5 1846 -1 1865 0 1894 -2 1927 0 1956 -4 1985 -3 2001 -4 2014 -3 2004 -10 1988 -10 1952 -14 1891 -15 1827 -19 1759 -12 1698 -10 1659 -9 1640 -7 1630 -6 1627 -15 1617 -11 1617 -3 1624 -2 1640 -6 1656 -21 6850 1 7241 1 1775 6 1836 4 1907 -1 1975 -3 2027 -5 2068 -2 2097 -3 2120 2 2146 -3 2159 0 2172 -15 2162 -10 2136 -17 2097 -13 2046 -14 1998 -11 1956 -10 1920 -9 1901 -13 1865 -13 1840 -7 1801 -9 1772 -9 1756 8 1766 -3 1785 -4 1824 -2 1872 3 1911 -1 1959 -1 1994 -1 2017 -5 2027 -8 2036 -1 2030 -6 2023 -5 2023 -5 2023 -4 2020 -5 2020 -8 2004 -12 1978 -14 1940 -8 1885 -10 1856 -8 1824 -9 1807 -10 1798 -13 1778 -13 1753 -11 1720 -15 1701 -11 1682 -13 1679 -3 1691 0];
u1=data1(1:2:299);
y1=data1(2:2:300);
u1=u1 ;
y1=y1 ;
bicycle1=iddata(y1,u1,1/15);
bicycle1.inputname= 驱动电压 ;
bicyclel.outputname= 车体倾角 ;
ze1=bicycle1(1:75);
figure,plot(ze1(1:75))
ze1=dtrend(ze1);
figure,plot(ze1(1:75))%figure,plot(ze1(50:200))
NN=struc(1:10,1:10,1:10); %生成多个模型结构参数
V=arxstruc(bicycle1(1:100),bicycle1(50:150),NN); %计算多个单ARX模型的损失函数
nn=selstruc(V, aic ); %确定阶次,选择模型结构
M=arx(ze1,[2,1,4]); %确定ARX模型参数
data2=[1724 0 1772 -2 1824 -2 1865 -2 1894 -5 1907 -3 1923 -1 1949 1 1981 -2 2017 -3 2049 -2 2062 -6 2062 -8 2059 -6 2043 -5 2023 -14 2001 -10 1975 -7 1949 -11 1923 -13 1904 -14 1885 -17 1856 -14 1827 -15 1804 -11 1782 -11 1775 -8 1785 -5 1817 9 1859 4 1901 0 1946 -3 1991 0 2030 -2 2065 -3 2088 -3 2104 -7 2104 -8 2094 -8 2081 -6 2068 -10 2049 -4 2027 -5 1994 -10 1956 -15 1901 -15 1836 -19 1766 -19 1691 -14 1646 -8 1627 -3 1627 -9 1624 -13 1608 -7 1588 7 1575 -8 1575 -13 1579 -7 1585 -2 1617 7 1688 10 1778 5 1878 0 1956 -2 2010 -2 2052 3 2085 -3 2110 0 2120 -12 2104 -7 2081 -9 2052 -7 2023 -10 1988 -7 1956 -13 1917 -21 1865 -17 1804 -21 1727 -16 1662 -10 1630 -4 1627 -14 1640 -6 1672 12 1727 7 1791 4 1856 -5 1898 -8 1907 -8 1911 -6 1904 -1 1917 -3 1927 -8 1940 -3 1962 0 1988 0 2023 0 2052 -3 2075 -6 2085 -5 2085 -7 2078 -8 2059 -7 2033 -11 2014 -13 1975 -16 1930 -18 1869 -20 1804 -18 1743 -13 1695 -10 1666 -2 1666 -14 1675 -21 1701 -4 1749 2 1811 0 1865 -3 1907 -2 1936 -6 1956 0 1972 2 1988 -1 2014 -3 2033 -4 2039 -4 2043 -5 2039 -7 2030 -4 2017 -9 1998 -9 1972 -10 1943 -15 1904 -17 1856 -19 1788 -13 1724 -11 1679 -9 1659 -6 1662 -3 1675 -5 1698 -1 1737 13 1778 1 1824 -3 1869 0 1923 -1 1959 -3 1985 -5 2001 -4];
u2=data2(1:2:299);
y2=data2(2:2:300);
u2=u2 ;
y2=y2 ;
bicycle2=iddata(y2,u2,1/15);
bicycle2.inputname= 驱动电压 ;
bicycle2.outputname= 车体倾角 ;
ze2=bicycle2(1:150);%ze2=bicycle2(1:150);
ze2=dtrend(ze2);
figure,plot(ze2(1:150))
figure,compare(ze2,M);
figure,resid(M,ze2);
ze=bicycle1(1:100);
%TimedomainPlot
th=arx(ze,nn);
th=sett(th,0.08);
u=z(:,2);
y=z(:,1)+ave;
yp=idsim(u,th)+ave;
xlb1= TimeStePs ;
subplot(2,1,1);
index=1:trn_data_n;
plot(index,y(index),index,yp(index), . );
rmse=norm(y(index)-yp(index))/sqrt(length(index));
title([ (a) Training Data (Solid Line) and ARX Prediction (Dots) with RMSE=
num2str(rmse)]);
disp([ [na nb d」=
num2str(nn)]);
xlabel(xlbl);
subplot(2,l,2);
index=(trn_data_n+1):(total_data_n);
plot(index,y(index),index,yp(index), . );
rmse=norm(y(index)-yp(index))/sqrt(length(index));
title([ (b) Checking Data (Solid Line) and ARX Prediction (Dots) with RMSE=
num2str(rmse)]);
xlabel(x1b1);
免责声明/版权申明 Passiontech
所有文章为网上搜集或私下交流学习之用,任何涉及商业盈利目的均不得使用,否则产生的一切后果由您自己承担!
本站仅仅提供一个观摩学习的环境,将不对任何资源负法律责任。所有资源请在下载后24小时内删除。
若无意中侵犯到您的版权利益,请来信联系我们,我们会在收到信息三天内给予处理!
url: http://www.51lm.cn/p/templates/cn/show.php?cid=905&aid=172


