基于动态模型的直接转矩控制技术仿真分析

1直接转矩控制的基本原理及规律

直接转矩控制系统简称DTC（Direct Torque Control）系统，是继矢量控制系统之后发展起来的另外一种高动态性能的交流电动机变压变频调速系统。在它的转速环里面利用转矩反馈直接控制电机的电磁转矩，因此而得名为直接转矩控制。

1.1直接转矩控制系统原理与特点

如图1-1为直接转矩控制的原理框图，和VC系统一样，它也是分别控制异步电动机的转速和磁链，转速调节器ASR的输出作为电磁转矩的给定信号，在后面设置转矩控制内环，它可以抑制磁链变化对于转矩的影响，从而使得转速和磁链系统实现解耦。因此，从整体控制结构上来看，直接转矩控制（DTC）系统和矢量控制系统（VC）系统是一致的都获得了较高质量的动态性能以及静态性能。

 

 

 

 

 

 

 

 图1-1直接转矩控制系统图

从图中中可以看出，直接转矩控制系统，就是通过使定转子磁链的幅值保持恒定，然后选择合理的零矢量的作用次序和作用时宽，以调节定子磁链矢量的运动速度，从而改变磁通角的大小，以实现对电机转矩的控制。在直接转矩控制技术中，其基本控制方法就是通过电压空间矢量来控制定子磁链的旋转速度，控制定子磁链走走停停，以改变定子磁链的平均旋转速度的大小，从而改变磁通角的大小，以达到控制电动机转矩的目的。

从以上介绍我们可以了解到DTC系统在具体控制方法上的一些特点：

⑴转矩和磁链的控制采用双位式控制器，并在PWM的逆变器中直接用这两个控制信号产生电压的SVPWM波形，从而避开了将定子电流分解成转矩和磁链分量，省去了旋转变换和电流控制，简化了控制器的姐结构。

⑵选择定子磁链作为被控制量，而不像VC系统中那样选择旋转磁链，这样一来，计算磁链的模型可以不受转子参数变化的影响，提高了控制系统的鲁棒性。如果从数学模型控制的规律，显然要比转子磁链定向时复杂的多。

⑶由于采用了直接转矩控制，在减速或负载变化的动态过程中，可以获得快速的转矩响应，但必须注意限制过大的冲击电流，以免损坏功率开关器件，因此实际的转矩响应也是有限的。

1.2直接转矩系统的控制规律和反馈系统

在DTC系统中采用的是两相静止坐标（αβ坐标），为了简化数学模型，由三相坐标变换成两相是非常重要的，所以可以避开旋转变换。由式（1-1）和式（1-2）可得

                        （1-1）

                          （1-2）

移项并积分后得

                                                           （1-3）

                                                           （1-4）

式（1-3）和式（1-4）就是图1-1中所采用的定子磁链模型，其结构框图如图2-2所示。它适合于中低速时切换到电流模型，这是上述能提高鲁棒性的优点就不得不丢弃。

 

 

 

 

 

 

 

 

                                 

                      图2-2 定子磁链模型结构框图 

在两相静止坐标系上的电磁转矩表达式为

                                        （1-5）  

整理可得

                                          （1-6）这就是DTC系统所用的系统模型，结构图如图1-3所示。

 

 

 

 

 

 

 

 

                     图1-3 转矩模型结构框图

2系统仿真分析

2.1仿真模型的建立

根据前文所述直接转矩控制基本原理，可以采用Simulink建立直接转矩如图2-1所示

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

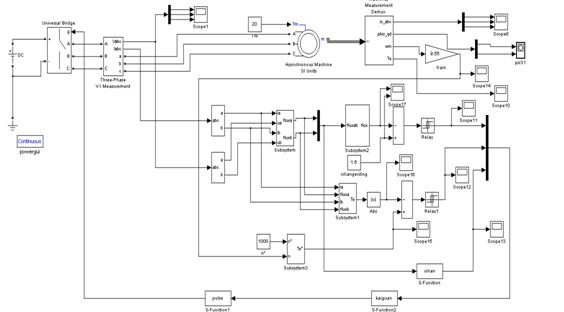
图2-1直接转矩系统仿真图

 

在这个仿真系统中拥有一下几个模块，分别是三相桥式逆变器、三相异步电动机、坐标变换（3/2）、定子磁链观测电路、PWM控制信号观测电路。

2.2坐标变换

三相电压在静止坐标系变换的表达式为：

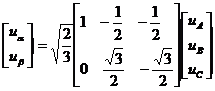            （2-1）

 

三相电流在静止坐标系变换的表达式为：

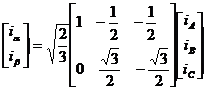            （2-2）

根据表达式（2-1）、（2-2）以及电机的参数可以得到三相电压电流在静止坐标系的仿真图，在图2-1中我们采用模块代替了这部分仿真电路，模块内部电路图如图2-2所示。

 

 

 

 

 

 

 

 

 

 

 

 

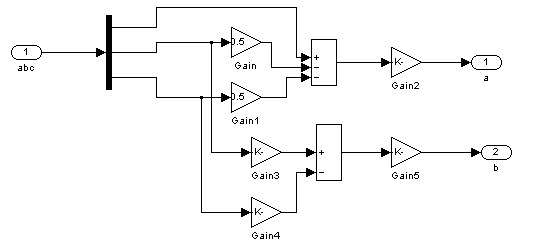
                         图2-2 3/2坐标变换仿真图

电路的输入为三相电压或者电流，经过电路的数学转换之后，最终在电路的a、b两端输出在静止坐标系下的电流（ ）或者静止坐标系下的电压（和）。

2.3定子磁链观测电路

在直接转矩控制系统中无论是按圆形轨迹控制还是采用六边形轨迹控制，都需要已知定子磁链。电机额定定子磁链的表达式为：

（2-3）

 

E——每相定子电势的有效值

f——定子频率

而在计算电机实际运行时的定子磁链是一般采用以下表达式：

                                                           （2-4）

 

介于观测定子磁链的重要性，在仿真图2-1中采用模块Subsystem代替了复杂的仿真电路的，基于定子电压电流和转速的磁链观测模型，模块Subsystem中的具体电路图如图2-3所示。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

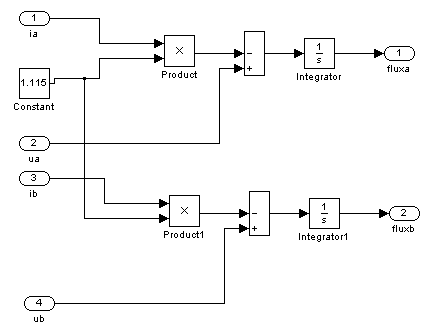
                 2-3磁链观测仿真电路

2.4 PWM控制信号生成模块

基于定子磁链的直接转矩控制系统的原理就是以定子磁链为控制对象，根据定子磁链的需要对电路的电压电流进行调整。在本次仿真中，对电流及电压的调整都需要对三相逆变电路进行调整，也就是需要对三相桥式逆变电路的6个开关管的开关频率及开关时间进行有目的性的控制。

在这次仿真过程中对于PWM波的产生采用了二维表格（表2-1）的方法得出，其中Ms为磁链信号，Ms=0表示减少磁链，Ms=1表示增加；磁链Ts为转矩信号，Ts=--1表示减少转矩，Ts=0表示保持转矩不变，Ts=1表示增加转矩；Fs为磁链所在扇区信号。

表2-1电压矢量选择表

Ms	Ts	Fs
		1	2	3	4	5	6
0	-1	U1	U5	U4	U6	U2	U3
	0	U0	U7	U0	U7	U0	U7
	1	U2	U3	U1	U5	U4	U6
1	-1	U5	U4	U6	U2	U3	U1
	0	U7	U0	U7	U0	U7	U0
	1	U6	U2	U3	U1	U5	U4

 

在本次仿真中采用了函数计算s-Function的方法来对来确定Ms、Ts以及Fs的数值，在仿真中s-function1和s-function2共同确定二维坐标系中的数值。

s-function1和s-function2中函数具体可见附录I。

2.5仿真结果

如图2-1中异步电机的仿真参数如图2-4所示，具体为:额定功率 Pn= 3730w , 额定线电压 Un = 460V, 额定频率fn = 50 Hz , 额定转速n=1460rpm,定子电阻Rs = 1.115Ω, 定子漏感 L1s = 0.005974H, 转子电阻Rr=1.803Ω,转子漏感L1 r = 0.005974H, 互感 Lm  0.2037H, 转动惯量 J =0.02kg·m², 摩擦系数 F = 0.005752

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

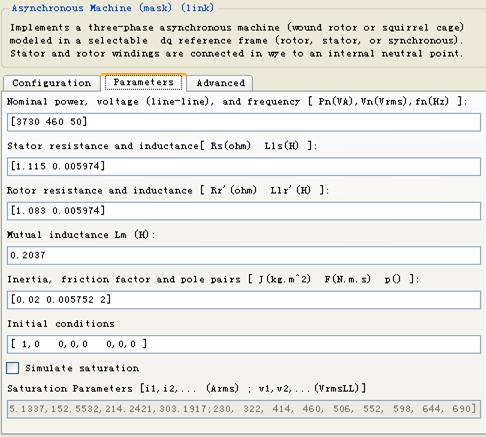
                   图2-4 异步电机仿真参数

在三相逆变器输出的三相电压电流会随着反馈回路磁链、转速以及转矩而发生变化，所以会出现一些波动，如图2-5为三相电流的输出波形。

 

 

 

 

 

 

 

 

 

 

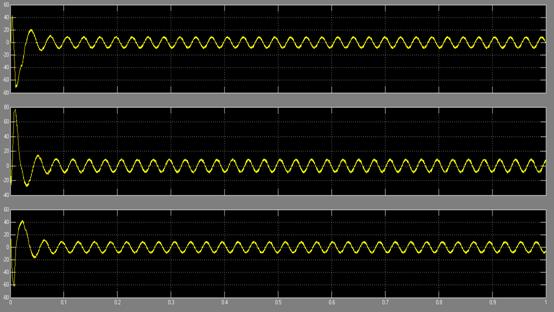
                        图2-5三相电流波形

由于直接转矩控制系统仿真是基于定子磁链的，所以整个控制的目的就是为了得到一个圆形的定子磁链，仿真结果定子磁链如图2-6所示。

 

 

 

 

 

 

 

 

 

                     图2-6定子磁链轨迹

直接转矩控制系统的输出转矩在调节过程中现会达到幅值，然后由于闭环反馈使得定子磁链维持圆形，输出转矩会逐渐靠近于给定转矩（Tm=20），但由于是动态模型所以会出现波动，具体波形如图2-7所示。

 

 

 

 

 

 

 

 

 

 

 

                          2-7 http://www.51lm.cn/p/templates/cn/show.php?cid=0&aid=219