MTanks
型号: PXF3293
MATLAB 7 (R14 SP2/SP3) MATLAB R2006a/b, R2007a
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

www.inteco.com.pl
NOTES
SAFETY OF THE EQUIPMENT
The equipment, when used in accordance with the supplied instructions, within the parameter set for its mechanical and electrical performance, should not cause any danger to health or safety if normal engineering applications are observed.
If, in specific cases, circumstances exist in which a potential hazard may be brought about by careless or improper use, these will be pointed out and the necessary precautions emphasised.
Some National Directives require to indicate on our equipment certain warnings that require attention by the user. These have been indicated in the specified way by labels. The meaning of any labels that may be fixed to the equipment instrument are explained in this manual.

Risk of electric shock
PRODUCT IMPROVEMENTS
The Producer reserves a right to improve design and performance of the product without prior notice.
All major changes are incorporated into up-dated editions of manuals and this manual is believed to be correct at the time of printing. However, some product changes which do not affect the capability of the equipment, may not be included until it is necessary to incorporate other significant changes.
ELECTROMAGNETIC COMPABILITY
This equipment, when operated in accordance with the supplied documentation, does not cause electromagnetic disturbance outside its immediate electromagnetic environment.
COPYRIGHT NOTICE
© Inteco Limited
All rights reserved. No part of this manual may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior permission of Inteco Ltd.
ACKNOWLEDGEMENTS
Inteco Ltd acknowledges all trademarks. IBM, IBM -PC are registered trademarks of International Business Machines. MICROSOFT, WINDOWS are registered trademarks of Microsoft Corporation. MATLAB and Simulink are registered trademarks of Mathworks Inc.
CONTENTS
1. INTRODUCTION AND DESCRIPTION ......................................................................... 7
1.1 SYSTEM OVERVIEW ........................................................................................................... 8
1.2 HARDWARE INSTALLATION .............................................................................................10
1.3 SOFTWARE INSTALLATION .............................................................................................. 10
2. STARTINGAND TESTINGPROCEDURES................................................................11
2.1 STARTING PROCEDURE .................................................................................................... 11
2.2 BASIC TESTS ....................................................................................................................12
2.3 TROUBLESHOOTING......................................................................................................... 15
2.4 STOPPING PROCEDURE..................................................................................................... 15
3. MULTITANK CONTROL WINDOW ............................................................................ 16
3.1 TOOLS ............................................................................................................................. 16
3.2 SIMULATION MODELS ......................................................................................................20
3.3 RTWT DEVICE DRIVER ................................................................................................... 22
3.4 DEMO CONTROLLERS ...................................................................................................... 25
4. MATHEMATICAL MODEL OF THE TANK SYSTEM ............................................. 28
4.1 LAMINAR OUTFLOW OF THE IDEAL FLUID ........................................................................ 30
4.2 MODEL OF A CASCADE OF N-TANKS................................................................................. 30
4.3 NONLINEAR MODEL OF THE THREE TANK SYSTEM: PUMP CONTROLLED SYSTEM ............. 31
4.4 LINEAR MODEL OF THE TANK SYSTEM ............................................................................. 34
4.5 DEFINITIONS OF CONTROL TASKS .................................................................................... 35
5. IDENTIFICATION............................................................................................................ 37
5.1 SENSOR CHARACTERISTIC CURVE ....................................................................................37
5.2 IDENTIFICATION OF VALVES ............................................................................................ 39
5.3 IDENTIFICATION OF PUMP ................................................................................................ 40
5.4 IDENTIFICATION OF PARAMETERS OF THE TANKS............................................................. 41
6. REAL-TIME CONTROL EXPERIMENTS ................................................................... 44
6.1 DESIGN OF LINEAR CONTROLLER..................................................................................... 44
6.2 FUZZY CONTROLLER ....................................................................................................... 49
7. PROTOTYPING AN OWN CONTROLLER IN RT-CON ENVIRONMENT........... 57
7.1 CREATING A MODEL ........................................................................................................ 59
7.2 CODE GENERATION AND BUILD PROCESS .........................................................................62
8. DESCRIPTION OF THE TANK CLASS PROPERTIES ............................................. 65
8.1 BASEADDRESS ................................................................................................................ 66
8.2 BIAS ................................................................................................................................ 67
8.3 BITSTREAMVERSION ....................................................................................................... 67
8.4 PWM .............................................................................................................................. 68
8.5 PWMPRESCALER ............................................................................................................68
8.6 PWMMODE .................................................................................................................... 69
8.7 VALVE............................................................................................................................. 70
8.8 PUMP...............................................................................................................................70
8.9 SCALECOEFF ...................................................................................................................71
8.10 TIME.............................................................................................................................. 71
8.11 SAFETYFLAG................................................................................................................. 72
8.12 SAFETYMAX ................................................................................................................. 72
8.13 SAFETYMIN................................................................................................................... 73
8.14 SAFETYALERT............................................................................................................... 73
8.15 THETANKCLASSQUICKREFERENCETABLE..................................................................74
9. REFERENCES...................................................................................................................75
1. INTRODUCTION AND DESCRIPTION
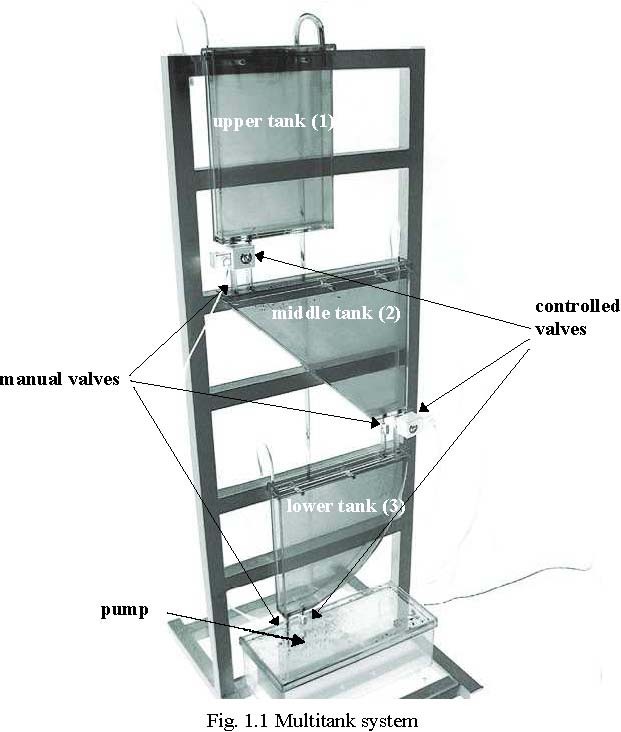
The Multitank System (MT) (Fig. 1.1) comprises a number of separate tanks fitted with drain valves. The separate tank mounted in the base of the set-up acts as a water reservoir for the system. Some of the tanks have a constant cross section, while others are spherical or conical, so having variable cross section. This creates main nonlinearities of the system. A variable speed pump is used to fill the upper tank. The liquid outflows the tanks due to gravity. The tank valves act as flow resistors. The area ratio of the valves is controlled and can be used to vary the outflow characteristic. Each tank is equipped with a level sensor based on hydraulic pressure measurement.
The Multitank System relates to liquid level control problems commonly occurring in industrial storage tanks. For example, steel producing companies around the world have repeatedly confirmed that substantial benefits are gained from accurate mould level control in continuous bloom casting. Mould level oscillations tend to stir foreign particles and flux powder into molten metal, resulting in surface defects in the final product [1].
The goal of the Multitank System design is to study and verify in practice linear and nonlinear control methods. The general objective of the control is to reach and stabilise the level in the tanks by an adjustment of the pump operation or/and valves settings. This control problem can be solved by a number of level control strategies ranging from PID to adaptive and fuzzy logic controls [2], [3], [4].
The Multitank System has been designed to operate with an external, PC-based digital controller. The control computer communicates with the level sensors, valves and pump by a dedicated I/O board and the power interface. The I/O board is controlled by the real-time software which operates in MATLAB®/Simulink RTW/® and RT-CON (INTECO product) rapid prototyping environment. This manual describes:
- the system,
- the installation of the multitank software,
- the mathematical models and theory related to control experiments,
- the identification procedures,
- how to use the library of ready-to-use real-time controllers,
- step-by-step how to design and apply ones own controller in the MATLAB/Simulink and RT-CON environment.
This is assumed that a user has an experience with MATLAB and Simulink from MathWorks Inc.
1.1 SYSTEM OVERVIEW
The tank system consists of a number of tanks placed above each other (Fig. 1.1). Some of the tanks have a constant cross section, while others are spherical or prismatic, so having variable cross section. Liquid is pumped into the upper tank from the supply tank by the pump driven by a DC motor. The liquid outflows the tanks only due to gravity. The output orifices act as flow resistors, but can also be controlled from the computer.
The levels in the tanks are measured with pressure transducers. The frequency signals of the level sensors are connected to the digital inputs of the RT-DAC/PCI multipurpose I/O board. There are four control signals send out from the board to the multitank system: three valve
Multitank System -User’s Manual
controls and one pump control signal. The appropriate PWM control signals are transmitted from digital outputs of the I/O board to the power interface, and next to the valves and to the DC motor. The speed of the pump motor is controlled by a sequence of PWM pulses configured and generated by the logic of XILINX chip of the RT-DAC board.
The liquid levels in the tanks are the system states. The general objective of the tank system control is to reach and stabilise a desired levels in the tanks by an adjustment of the pump operation and/or valves settings. For the real system the levels in the tanks as well as the flow rates of the pump are limited.
To use the multitank system the following software and hardware components are required:
• Intel Pentium compatible PC with:
- Windows 2000/XP,
- MATLAB version 7 (R14 SP2/SP3), R2006a/b or R2007a with Simulink and RTW toolboxes (not included),
- 32 bit compiler MS Visual C ++ or Open Watcom 1.3,
- RT-DAC/PCI programmable Input/Output board to be installed in the PC (included),
• CD-ROM including the multitank software and e-manuals (in pdf format):
- Installation Manual
- User’s Manual
The MT Toolbox supports MATLAB 7 (R14 SP2, SP3), MATLAB R2006a/b
- and R2007a with the MS Visual C++ 6.0 or OpenWatcom 1.3 compilers.
- Neither MATLAB nor the compiler (OpenWatcom or MS Visual C++) can be installed in Program Files directory (name of the directory cannot includes
- space).
- The experiments and corresponding to them measurements have been conducted by the use of the standard INTECO systems. Every new system manufactured and developed by INTECO can be slightly different to those
- standard devices. It explains why a user can obtain results that are not identical to these given in the manual.
1.2 HARDWARE INSTALLATION
Hardware installation is described in the Installation Manual.
- SOFTWARE INSTALLATION
- STARTING AND TESTING PROCEDURES
Insert the installation CD and proceed step by step the displayed commands.
2.1 STARTING PROCEDURE
Invoke MATLAB by double clicking on the MATLAB icon. The MATLAB command window opens. Then simply type:
Tank3
MATLAB brings up the Multitank Control Window (see Fig. 2.1).The user has a rapid access to all basic functions of the Multitank control and simulation systems from the Multitank Control Window. It includes tests, drivers, models and application examples.
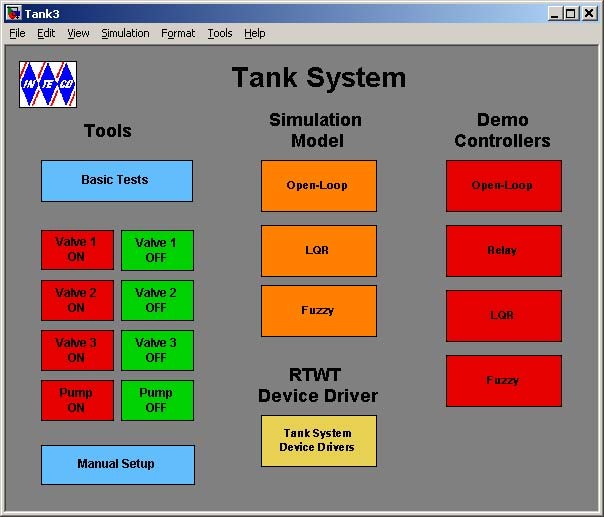
The Servo Control Window contains testing tools, drivers, models and demo applications. See section 4 for detailed description.
2.2 BASIC TESTS
This section explains how to perform the basic tests checking if mechanical assembling and wiring has been done correctly. The tests have to be performed obligatorily after assembling of the system. They are also necessary if any incorrect operation of the system was detected. The tests have been designed to validate the existence and sequence of measurements and controls. They do not relate to accuracy of the signals.
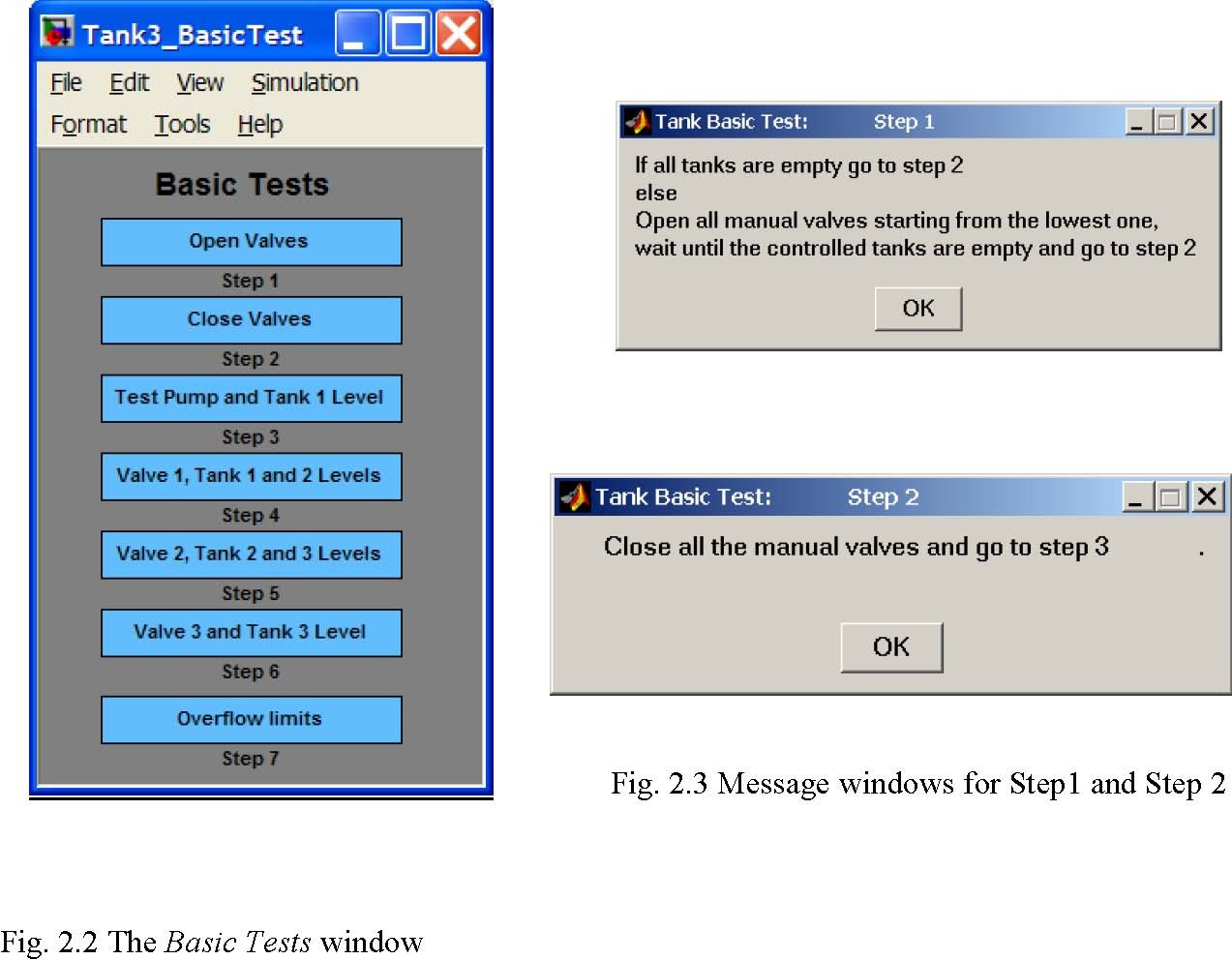
Seven testing steps are applied. The procedures allow user to check the pump operation, three controlled valves, three level sensors and overflow limits.
- Double click the Basic Tests button. The window given in Fig. 2.2 appears.
- The Step 1 and Step 2 prepare system for testing. You must start tests with empty tanks and closed valves. After clicking on Step 1 and Step 2 buttons the messages shown in Fig. 2.3 are displayed.
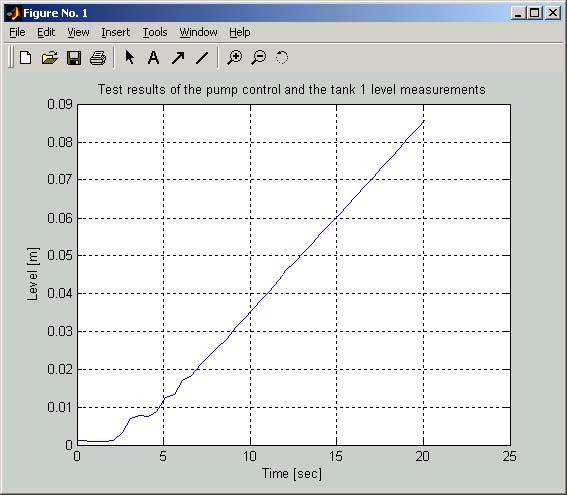
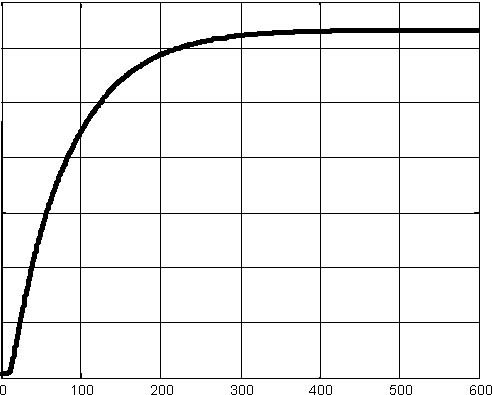
- In the Step 3 you can check if the pump works properly and if level in the tank 1 is measured correctly. After clicking Test Pump and Tank 1 Level button the pump starts and works 20 seconds. Then the pump is stopped and the liquid level in the tank 1 is plotted ( Fig. 2.4 ).
- In the Step 4 the valve in the tank 1 opens and the levels in the tanks 1 and 2 are measured. The measurements are plotted (Fig. 2.5).
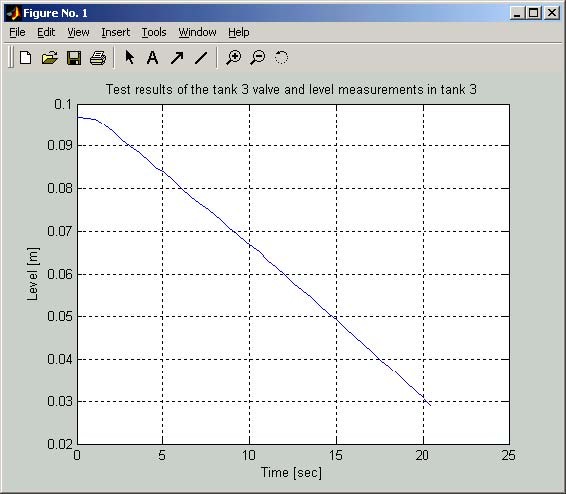
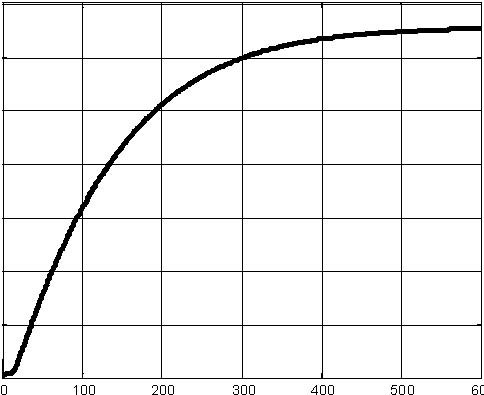
- In the Step 5 the valve 2 is opened and the levels in the tanks 2 and 3 are measured. Results are shown in Fig. 2.6.
- In the Step 6 the valve 3 is opened and the level in the tank 3 is measured. The results are shown in Fig. 2.7.
- In the step 7 the logical limit switches built into the FPGA chip structure (RT-DAC 4 I/O board) are tested. The task of these “emergency” switches is to turn off the pump if the overflow in any of the tanks occurs. When the pump is turned off and the level in the tank falls down under the emergency limit the pump starts again. Close the manual valve in the tank 1 and click Overflow limits button. The pump starts and works until the level in tank 1 becomes equal to the value pre-set in the FPGA chip.


To finish the tests click the Pump off button in the MultiTank Main Window to set the pump control to zero.
2.3 TROUBLESHOOTING
| Problem | Solution |
| System does not work | Check if the RTDAC/PCI board is properly installed. Check if the power interface is “on”. Check if hardware stop button is released. |
| Pump does not work | Check the cable connection between the pump and the power interface. Overflow alert – empty the water out of tank. |
| Valve does not open | Check the cable connection between the valve and the power interface. Overflow alert – empty the water out of tank. |
| Level measurements are not correct | Check the cable connection between the level sensors and the power interface. Check if the rubber pipe is connected to the sensor and to the metal pipe in the tank. |
2.4 STOPPING PROCEDURE
The system is equipped with the hardware stop pushbutton. It cuts off the transfer of control signals to the tanks. The pushbutton does not terminate the real-time process running in the background on PC. Therefore, to stop the task you have to use Simulation/Stop real-time code pushbutton from the pull-down menus in the model window.
3. MULTITANK CONTROL WINDOW
The user has a quick access to all basic functions of the multitank system from the Multitank Control Window. It includes tests, drivers, models and application examples.
Type at Matlab prompt Tank3 command and Multitank Control Window presented in Fig. 2.1 opens.
The Multitank Control Window contains menu items divided into four groups:
- Tools -Basic tests and Manual Setup,
- Simulation Models,
- RTWT Device Driver,
- Demo Controllers.
3.1 TOOLS
The respective buttons in the TOOLS column perform the following tasks:
Basic Tests -checks the fluid levels measurements, DC pump operation and controlled valves operation. The Basic Tests tool is described in details in section 3.2.
Valve 1 ON – fully opens the valve of the first (upper) tank,
Valve 1 OFF – fully closes the valve of the first (upper) tank,
Valve 2 ON – fully opens the valve of the second (middle) tank,
Valve 2 OFF – fully closes the valve of the second (middle) tank,
Valve 3 ON – fully opens the valve of the third (lower) tank,
Valve 3 OFF – fully closes the valve of the third (lower) tank,
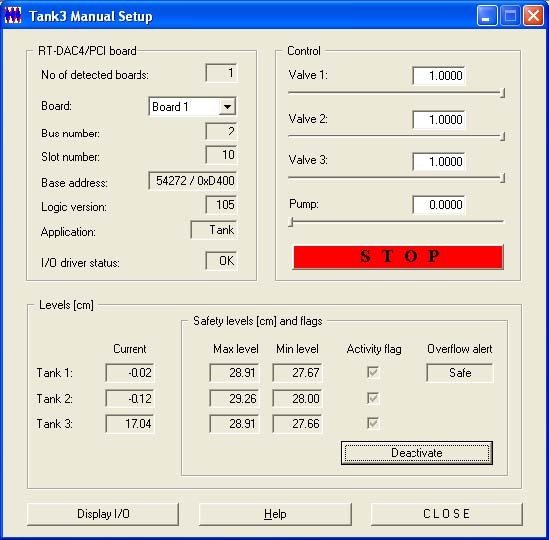
Manual Setup – opens the window giving access to the basic parameters of the laboratory 3tank setup. The most important data transferred from the RT-DAC/PCI board and the measurements of the multitank system as well as status signals and flags may be shown. Moreover, the control signals of three valves and the pump may be set manually (Fig. 3.1).
The application contains four frames:
- RT-DAC/PCI board
- Control
- Levels
- Safety levels and flags
The RT-DAC/PCI board frame presents the main parameters of the PCI board. The Control frame allows to change the control signals. The current liquid levels are given in the Levels frame. The Safety levels and flagsframe contains the maximum and minimum liquid levels, the state of the safety flag and the state of the overflow alert.
The Display I/O pushbutton activates the window that presents the contents of all RTDAC/4PCI input registers.
All the data presented by the Tank Manual Setup program are updated 10 times per second.
• RT-DAC/PCI board
The frame contains the parameters of the RT-DAC/PCI boards detected by the computer.
No of detected boards
Presents the number of detected RT-DAC/PCI boards. If the number is equal to zero it means that the software has not detect any RT-DAC/PCI board. When more then one board is detected the pull-down board list must be used to select the board connected with the program.
Board
Contains the list applied for selection of the board currently used by the program. The list contains a single entry for each RT-DAC/PCI board installed in the computer. A new selection executed at the list automatically changes values of the remaining parameters within the frame. If more then one RT-DAC/PCI board is detected the selection at the list must point to the board applied to control the multitank system. Otherwise the program is not able to operate in a proper way.
Bus number
Shows the number of the PCI bus where the current RT-DAC/PCI board is plugged-in. The parameter may be useful to distinguish boards, when more then one board is used and the computer system contains more then single PCI bus.
Slot number
It is the number of the PCI slot where the current RT-DAC/PCI board is plugged-in. The parameter may be useful to distinguish boards, when more then one board is used.
Base address
Contains the base address of the current RT-DAC/PCI board. The RT-DAC/PCI board occupies 256 bytes of the I/O address space of the microprocessor. The base address is equal to the beginning of the occupied I/O range. The I/O space is assigned to the board by the computer system and may differ from computer to computer. The base address is given in the decimal and hexadecimal forms.
Logic version
Displays the number of the configuration logic of the on-board FPGA chip. A logic version corresponds to the configuration of the RT-DAC/PCI board defined by this logic and depends on the version of the tank model.
Application
The name of the application taken from the on-board FPGA chip. A name of the application corresponds to the configuration of the RT-DAC/PCI board.
I/O driver status
Shows the status of the driver that allows the access to the I/O address space of the microprocessor. The status has to be OK string. In other case the Multi-Tank software HAS TO BE REINSTALLED.
• Control
The frame allows to set the control signals of three valves and to set the control signal for the pump.
Valve 1, Valve 2, Valve 3, Pump
The control signals of the valves and the pump may be set by entering a new value into the corresponding edit fields or by moving the corresponding slider. The control values may vary from 0.0 to +1.0. The value of 0.0 and +1 mean respectively: the zero control and the maximum control. If the valves are considered the zero control means that the valve is closed however the maximum control fully opens the corresponding valve. For the pump the flow increases when the control value changes from 0.0 to 1.0. If a new control value is entered into the edit field the corresponding slider changes respectively its value. If a slider is moved the value in the corresponding edit field changes as well.
STOP
The pushbutton is applied to switch off all the control signals. When pressed all the control values are set to zero.
• Levels
The frame presents the levels of liquid in three tanks. The levels are scaled in centimeters.
Within this frame the safety system parameters are given as well.
Safety levels and flags
There are maximum and minimum liquid levels associated with each tank. If in any tank the liquid level is higher then the maximum level the RT-DAC/PCI board automatically activates the overflow alert. If the overflow alert is active the RT-DAC/PCI board switches off all the control signals. During the overflow alert the valves are closed and the pump is off regardless of the control signals.
The overflow alert is disabled if the levels in all tanks are lower then the minimum levels. As during the overflow alert the automatic valves remain closed it is required to open manual valves to lower the liquid level below the minimum level.
Max level, Min level
The maximum and minimum levels of the liquid in the tanks. The levels are given in centimeters.
Activity flag
The state of the flags that enable the safety system for the respective tank.
Overflow alert
The state of the overflow alert. It displays the SAFE message if the overflow flag is inactive. The ALERT message indicates that the alert system is active.
Deactivate / Activate
The pushbutton deactivates the safety flags of all tanks for 15 seconds. If the safety flags are inactive the pumps and the valves operate regardless the liquid levels. The deactivation allows manual decreasing of the levels below the minimum safety levels. When the deactivation is in progress the caption of the button changes from “Deactivate” to “Activate”. The safety flags are activated back immediately after the “Activate” button is pressed.
3.2 SIMULATION MODELS
In this group some examples of simulation models are given. These models can be used to familiarise the user with the tank system operation and give templates for developing and testing the user-defined control algorithms. Only one model is described below. Other examples are given in Section 7.
After clicking on the Open-Loop button the model appears (Fig. 3.2).

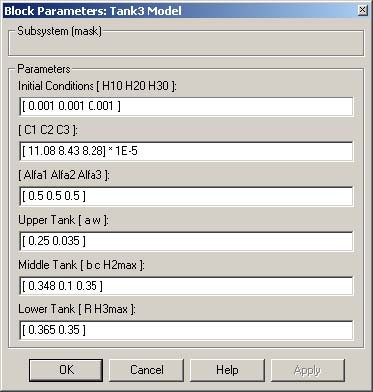
The mask of the Tank3 Model block is given in Fig. 3.3. All parameters of the tank system model significant for control are available in this window. They correspond to the mathematical model of the tank system.
The description of the parameters is given in the Section 5. Notice, that some parameters are fixed (e.g. geometry of tanks), while other must be identify and introduced , according to the current setting of the valves.
| x 10-5 | ||||||
|---|---|---|---|---|---|---|
| 3.5 | ||||||
| 0.08 | ||||||
| 3 | ||||||
| 0.07 | ||||||
| 2.5 | ||||||
| Pu | 0.06 | |||||
| mp | ||||||
| co | 2 | |||||
| ntr | 0.05 | |||||
| ol | H1 | |||||
| [m | 1.5 | [m] | ||||
| 3/s | 0.04 | |||||
| ] | 1 | |||||
| 0.03 | ||||||
| 0.5 |
|
|||||
| 0.02 | ||||||
| 0 | ||||||
| 0.01 | ||||||
| -0.5 0 100 | 200 300 400 500 | 0600 | ||||
| Time [s] | 0 100 | Time [s] 200 300 400 500 | ||||
0.14
0.12
0.12
0.1
0.1
0.08
H3 0.08
H2
[m] [m]
0.06
0.06
0.04
0.04
0.02
0.02
0 0
Time [s] Time [s]
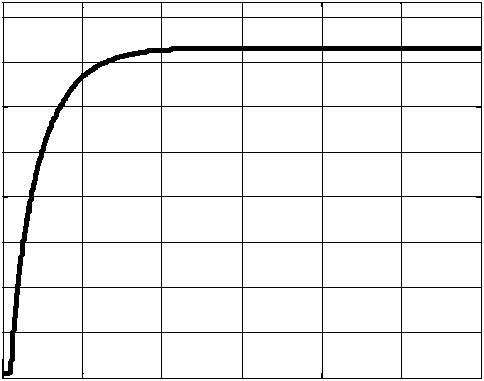
Fig. 3.4 Example of the step response simulation
3.3 RTWT DEVICE DRIVER
The main driver is located in the RTWT Device Driver group. The driver integrates MATLAB/Simulink environment and RT-DAC/PCI board transforming and transmitting measurement and control signals from/to the tanks system. If a user wants to build his own application he must copy this driver to a new model.
After clicking the Tank System Device Drivers button the window shown in Fig. 3.5 opens.
The driver has four PWM inputs. The first input (Pump) controls the DC pump. The inputs Valve1, Valve2 and Valve3 control the valves of the upper, middle and lover tanks. There are three analog outputs of the driver:Level1, Level2, Level3 and one digital output: Alert. Each analog output represents the liquid level in the tank displayed in metric units.
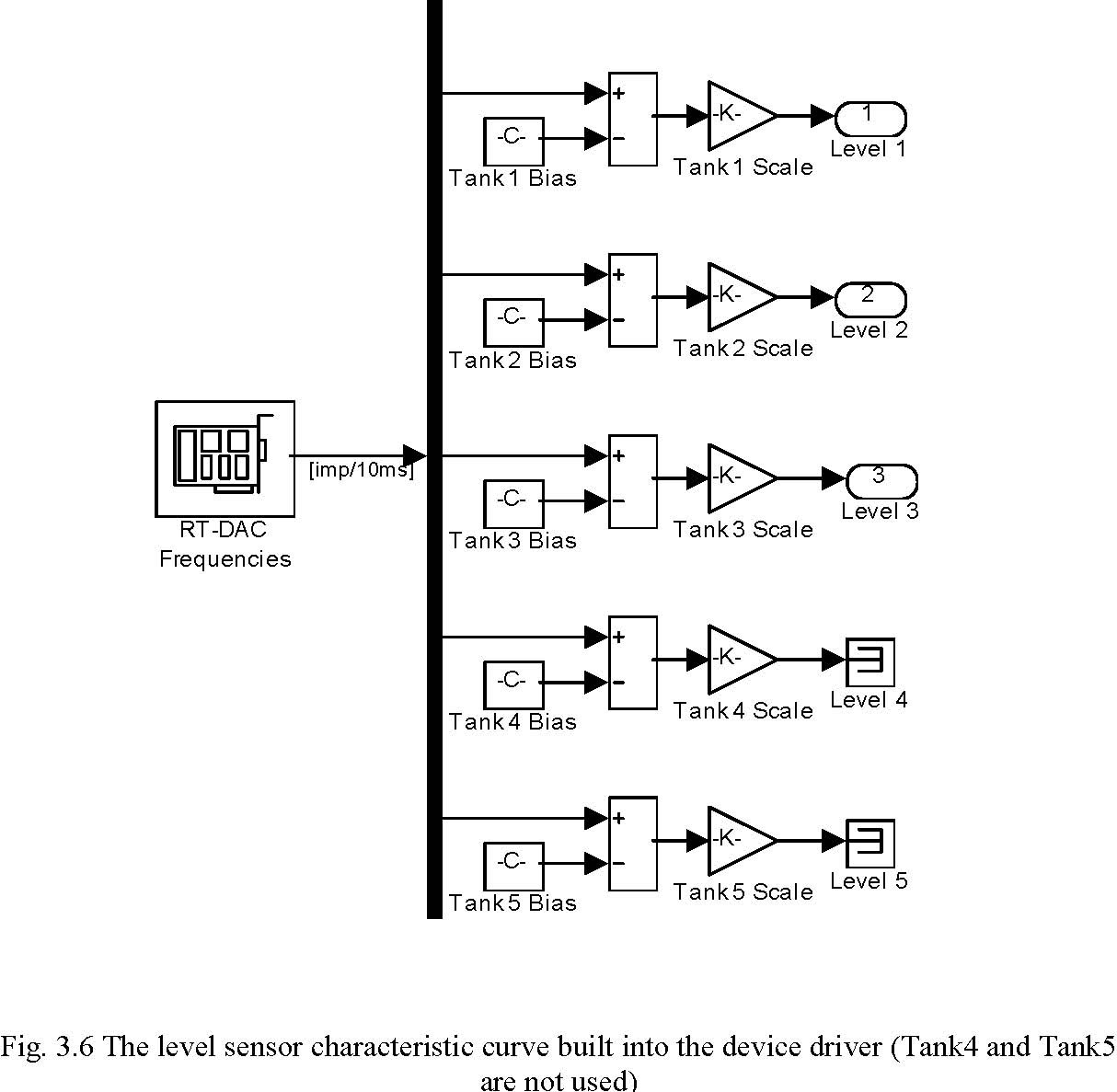
The frequency signal of the level sensor is prescaled to the metric units inside the device driver block (Fig. 3.6). Each level sensor is described by two parameters: Gain and Bias (see Section 5.1). These parameters should not be changed inside the device driver. To modify a parameter of the level sensor characteristic curve the following commands should be type in MATLAB command window:
>> aux = tank; % Creating object aux of the tank class
>> set(aux,’ScaleCoeff’,[0.0380 0.0380 0.0380 0.0 0.0]); % Changing the Gain parameters. The first value of the vector corresponds to the Gain parameter of the upper level sensor characteristic, etc (see section 5).
>> set(aux,’Bias’,[0.0020 0.0020 0.0020 0.0 0.0]); % Changing the Bias parameters. The first value of the vector corresponds to the Bias parameter of the upper level sensor characteristic, etc.
Example. Change Gain parameter of the upper level sensor characteristic to 0.034 and Bias parameter of the lower level sensor characteristic to 0.0021. >> aux = tank; >> OldGain = get(aux,’ScaleCoeff’); % Reading the old Gain parameters >> OldGain (1) = 0.034; % Modifying the first Gain >> set(aux,’ScaleCoeff’,OldGain); % Writing the new parameters >> OldBias = get(aux,’Bias’); % Reading the old Biasparameters >> OldBias(3) = 0.0021; % Modifying the third Bias >> set(aux,’Bias’,OldBias); % Writing the new parameters
This way can change parameters only temporary. To change them permanent the parameters must be saved in the TankV2PU_Coeff.m4 file. This file is located in the matlabroot/toolbox/Multitank/m/ directory. The parameters are read from this file. To see the variables stored in this file type the commands:
>> load -mat TankV2PU_Coeff.m4
>> who
Your variables are: TankBias TankScaleCoeff
>>size(TankBias)
ans= 1 5
Length of the TankBias and TankScaleCoeff variables is 5. Only three elements are used but five must be stored (the two last elements are prepared for future using).
The command to store permanently new parameters is as follows:
save matlabroot/toolbox/Multitank/m/TankV2PU_Coeff.m4 TankBias TankScaleCoeff -V4;
RT-DAC Frequencies
Do not make any changes inside the original driver. They should be made only inside its copy.
The C source code of the all components of the driver is included in the DevDriv directory.
3.4 DEMO CONTROLLERS
In this group the preprogrammed examples of the tank control systems are given. These demos can be used to familiarize the user with the tank system operation and help to create the user-defined control algorithms. Before starting an experiment real-time executable file must be created by pressing Tools/Real-Time Workshop/Build Model item in the Tools pull-down menu.
Due to similarity of the examples we focus our attention on one of them.
After clicking on the Relay button the model of simple, relay-controlled tank system appears (Fig. 3.7).
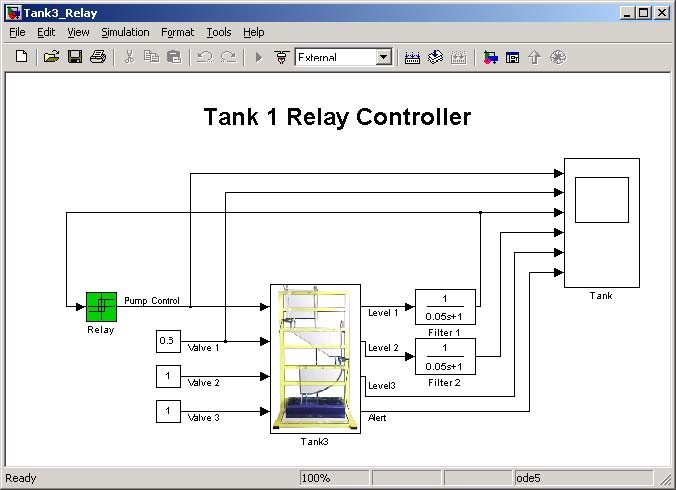
Notice, that this model looks like a typical Simulink model. The device driver given in Fig.
3.7 is applied in the same way as other blocks from the Simulink library. The only difference consists in applying the Real Time Windows Target (RTWT) to create the executable library which runs in the real-time mode.
The only goal of the control is to stabilize the liquid level in the upper tank by the relay controller. The valves control signals for the upper, middle and lower tanks are set to: 0.6, 1.0,
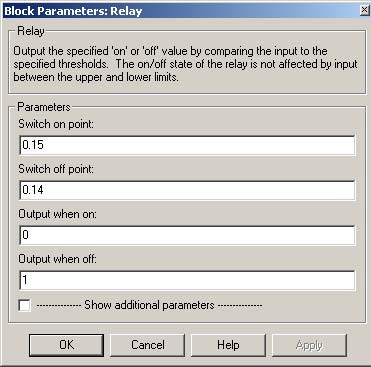
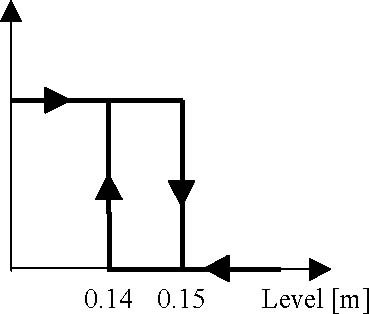
1.0 respectively. The mask of the Relay block is given in Fig. 3.8. The characteristic corresponding to the relay controller is presented in Fig. 3.9.
1
0
Fig. 3.9 Relay controller characteristic curve
Notice, that the control generated by the controller takes two values: 0 and 1. The switching limits are 0.15 m and 0.14 m. It means that the liquid level will be changed between these limits (except beginning of experiment, relative to initial conditions) with the speed corresponding to the operation of DC pump and Valve1 fixed settings. (equal to 1 and 0.6 respectively).
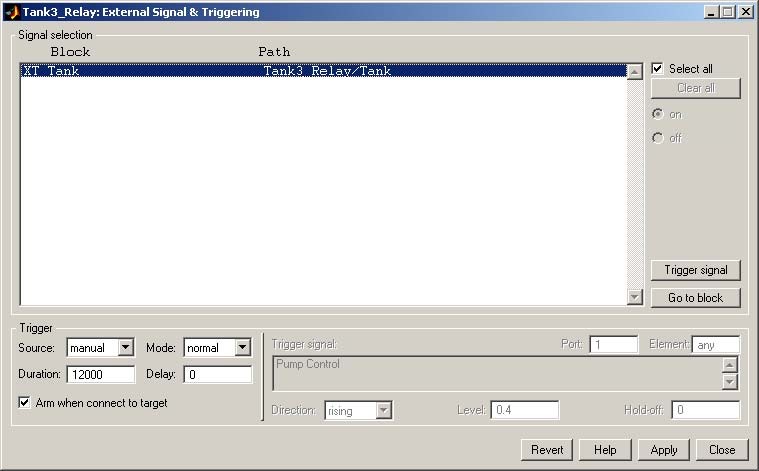
- To prepare data acquisition click the Tools/External Mode Control Panel… item, after click the Signal Triggering button. The window given in Fig. 3.10 opens.
- Select XT Tank , set Source as the manual option, mark Arm when connect to Target option and close the window.
- To start experiment choose the Tools pull-down menus in the Simulink model window. The pop-up menus provide a choice between predefined items. Choose the RTW Build item. A successful compilation and linking process is finished with the following message:
Successful completion of Real-Time Workshop build procedure for model Tank3_Relay
If any error occurs then the message corresponding to the error is displayed in the MATLAB command window.
• Return to the model window and click the Simulation/Connect to Target option. Next, click the Simulation/Start real-time code item.
PWM control signal
• After while observe the plots in the scope and click Stop Simulation after some time. The results of the experiment are shown in Fig. 3.11.
-5
x 10
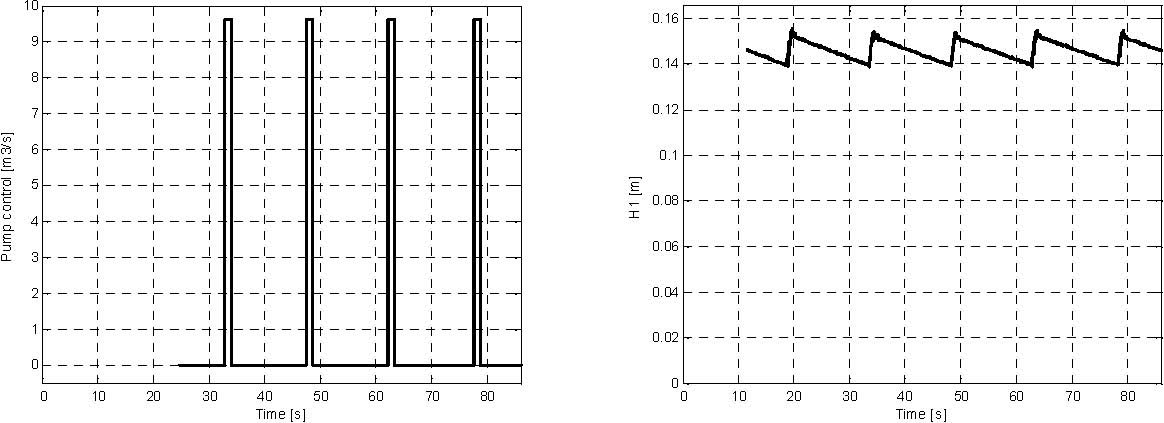
Fig. 3.11 Results of the relay controller demo real-time-experiment.
The liquid in the upper tank starts from 0.0 m level and oscillates between 0.14 m and 0.15 m levels. The DC pump control signal is the square wave in the range [0, 1].
Parameters, characteristic curves and plots given in the manual and introduced into Simulink demo models are only examples.
Therefore, it is recommended to identify the current system parameters before starting own experiments.
4. MATHEMATICAL MODEL OF THE TANK SYSTEM
Modern methods of design of advanced controllers usually require high quality models of the process. The classical procedure of a model development consists of the following steps:
- development of the mathematical model based on physics of the process,
- simplification of the model and/or its transformation into a standard form,
- development of a simulation model,
- tuning of the model parameters (identification),
- practical verification of the model.
q
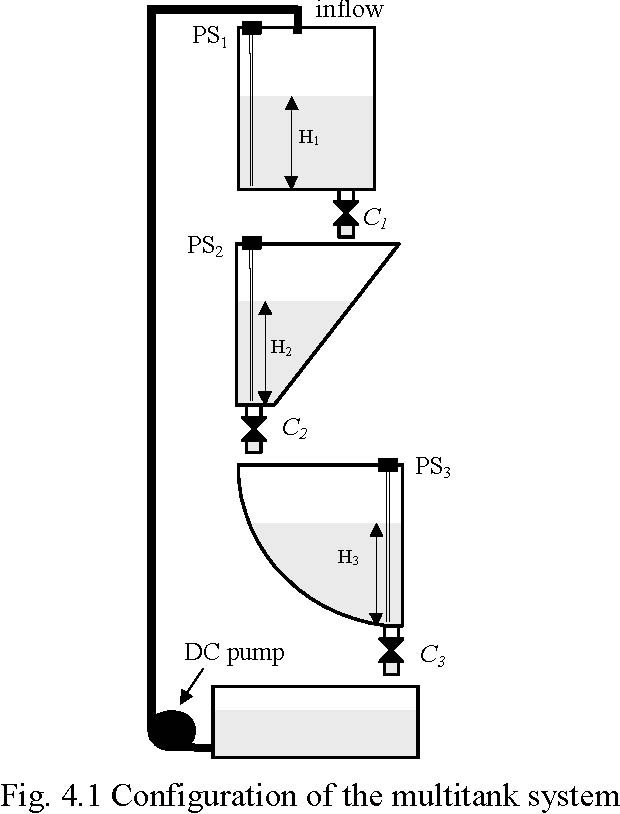
In the next sections we will execute the steps given above for the multitank system. Liqiud levels H ,H ,H in the tanks are the state variables of the system (Fig. 4.1). For the
123
tank system there are four controlled inputs: liquid inflow q and valves settings C ,C ,C .
123
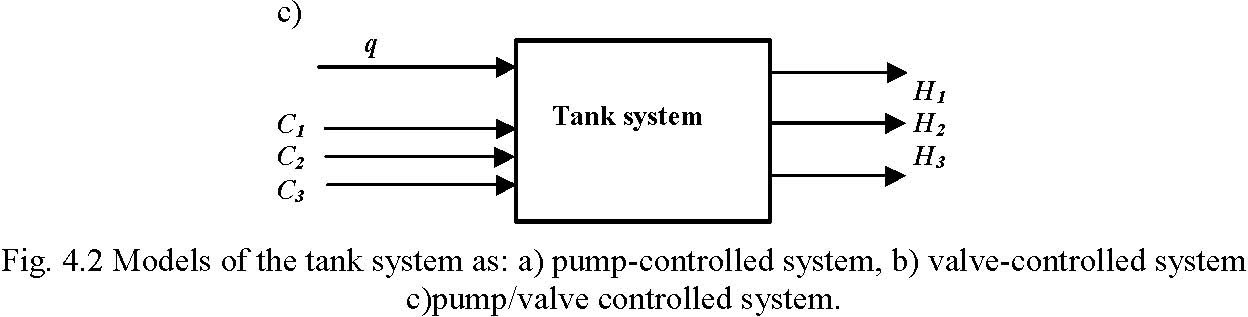
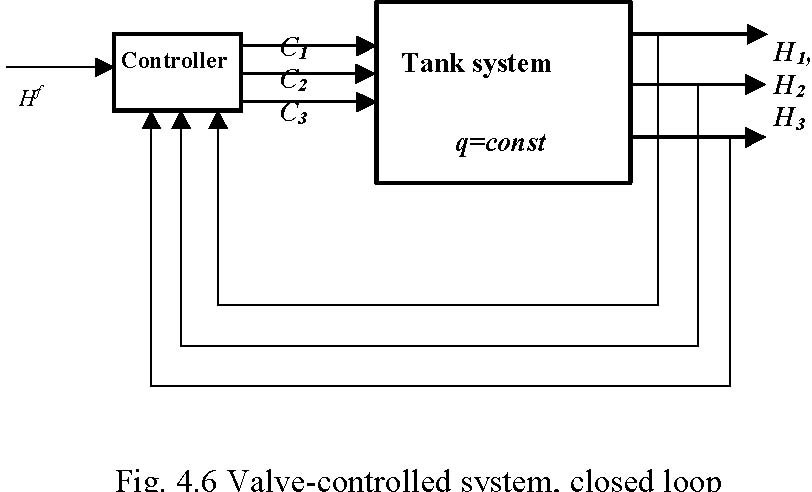
Therefore, several models of the tanks system can be analysed (Fig. 4.2), classified as pump-controlled system, valve-controlled system and pump/valve controlled system.
b)
C1 C2 C3 H1, H2 H3
 H1 H2 H3
H1 H2 H3
q
parameters
Several issues have been recognised as potential impediments to high accuracy control of level or flow in the tanks:
- nonlinearities (smooth and nonsmooth) caused by shapes of tanks,
- saturation-type nonlinearities, introduced by maximum or minimum level allowed in tanks,
- nonlinearities introduced by valve geometry and flow dynamics,
- nonlinearities introduced by pump and valves input/output characteristic curve.
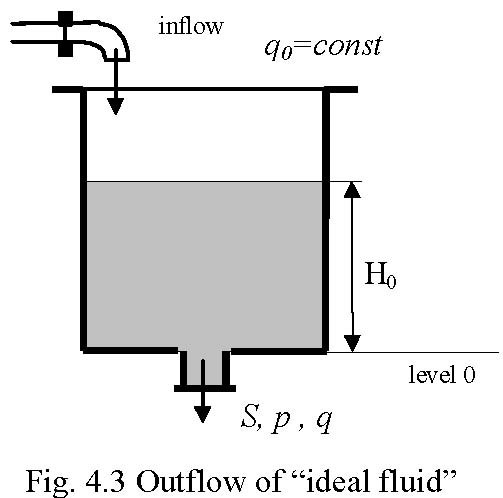
4.1 LAMINAR OUTFLOW OF THE IDEAL FLUID
The laminar outflow rate of an “ideal fluid” from a tank (Fig. 4.3) is governed by the Bernoulli law. This equation is obtained by a simple calculation of the potential and kinetic energy of the fluid [5]
Qr =µS ![]() 2gH 0 (5.1)
2gH 0 (5.1)
where: S– is the output area of the orifice, µ -is the orifice outflow coefficient.
4.2 MODEL OF A CASCADE OF N-TANKS
Assuming the laminar outflow of an “ideal fluid” for a cascade of n-tanks, the model describing dynamics of the process can be obtained by means of mass balance
dV
1 = q − C1 ![]() H1 dt
H1 dt
dV 2
= C![]() H − C
H − C![]() H (5.2)
H (5.2)
11 22
dt
…………………………..
dV n = C![]() H − C
H − C![]() H ,
H ,
n−1 n−1 nn
dt
where: V1,V2, K,Vn – fluid volumes in the tanks,
C1,C2, K,Cn – resistance of the output orifice,
H1,H2, K,Hn – fluid levels in the tanks, q – inflow to the upper tank. From equations (5.2) we obtain
dV 1 dH
1 = q − CH α1 , dH 1 dt 1
dV 2 dH 2 α1 α2
= C1H1 − C2 H2 , (5.3)
dH 2 dt
……………………………….
dV n 1
dH n αn−αn
= CH − CH .
n−1 n−1 nn
dH n dt
As mentioned above, for the laminar flows the outflow rate from a tank is governed by the Bernoulli law. In this case αi=1/2. For the real configuration of tanks, tubes and valves, if turbulence and acceleration of the liquid in the tube can not be neglected, a more general coefficients αi are applied.
4.3 NONLINEAR MODEL OF THE THREE TANK SYSTEM: PUMP CONTROLLED SYSTEM
Using the equations (5.3) for n=3 the nonlinear model of tank system from Fig. 4.2 is obtained
dH 11 α
1 = q − C1H11 dt β1(H1) β1(H1)
dH 11
2 α1 α2
= CH − CH (5.4)
11 22
dt β2(H2) β2(H2)
dH 31 α21 α3
= CH − CH
22 33
dt β (H ) β (H )
33 33
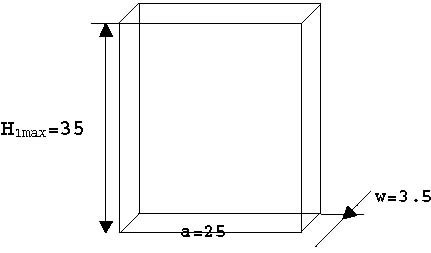
where: Hi -fluid level in the i tank, i = 1,2,3. βi(Hi) -cross sectional area of i tank at the level Hi, defined as: β1 (H1 )= aw -constant cross-sectional area of the upper tank,
H 2
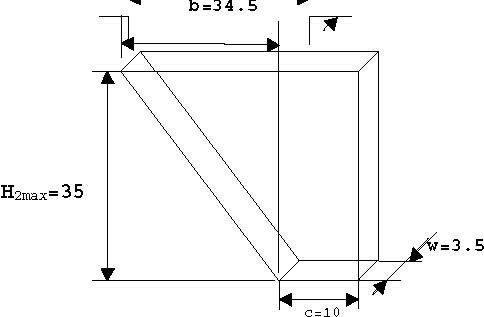
β2 (H 2 ) = cw + bw -variable cross sectional area for the middle tank,
H
2 max
2
β(H )= w![]() R −(R − H )2 -variable cross sectional area of the lower tank,
R −(R − H )2 -variable cross sectional area of the lower tank,
33 3
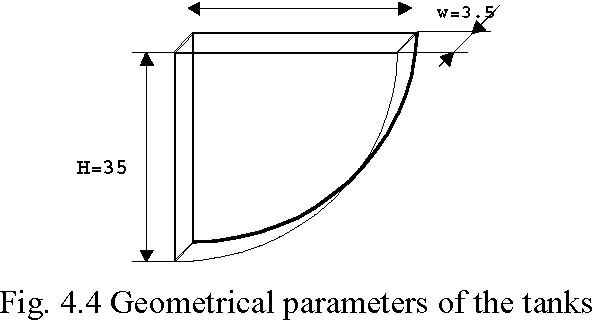
CI -resistance of the output orifice of i tank, αi -flow coefficient for i tank. Geometrical parameters [cm] of the tanks are given in Fig. 4.4.
R=36.4
Let us assume that pump-control system is considered.
Rewrite the right sides of equations (5.4) in the form F( x,q) = [F,F,F ] , where
123
F (q, H ) = 1 q − 1 CH α1
11 11
β (H ) β (H )
11 11
11
α1 α2
F (H , H ) = CH − CH (5.5)
212 11 22
β (H ) β (H )
22 22
1 α21 α3
F (H , H ) = CH − CH
323 22 33
β3(H3) β3(H3)
The model (5.4), for given initial conditions and control, describes the dynamics of the process on the set of model-admissible states
M
ℵ ={H :β (H ) ≠ 0,H ≥ 0}, i = 1,2,3,
i iii i
while process-admissible states of the process are usually determined as
P
ℵ ={H:0 ≤ H ≤ H } i = 1,2,3.
i
i i imax
Remark 1. The shapes of the tanks are such regular that the functions F1,F2 ,F3 are continuous and differentiable on ℵiM .
The admissible set of the control is given in the form Q ={q: 0 ≤ q ≤ qmax }.
Remark 2. In the most cases the set of process-admissible states can be obtained as a closure of the set of admissible states of the model : ℵiP =ℵiM .
For the model (5.4), for fixed q = q0 we can define an equilibrium state (steady-state points), given by
P
H = {H : F (q , H )= 0,.. F (H , H )= 0, i = 2..3}, q ∈Q, H ∈ℵ
0 i 10 1 ii−1 i 0 ii
The equilibrium states can be calculated from the equations
αα2 αn
1
q = CH = CH = ... = CH , (5.6)
0 110 2 20 nn0
or
1 1
α α1
q
⎛⎜⎜⎝
⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢
⎥⎥⎥⎥⎥⎥⎥⎥⎥
=
⎛⎜⎜⎝
⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢
q
⎥⎥⎥⎥⎥⎥⎥⎥⎥
1
0 0
⎜⎜
⎟⎟⎠
1
⎜⎜
⎟⎟
C1 C1
H
α α
10 1
⎢⎢⎢
⎥⎥⎥
α
C1
H
q
.
2 2
020
H
H =
=
⎜⎜
⎟⎟
⎜⎜
⎟⎟
10
0
C
C
M
2 2
M
M
H
α
1
n0
−1
n n
α
α
C
q
0
n
−1
H
n
⎟⎟
⎟⎟
n−1,0
C
Cn
n
Assumption 1
Any admissible q0 the corresponding H0 is state-admissible.
In the laboratory practice this assumption can be achieved by a proper setting of C1..C3 parameters.
4.4 LINEAR MODEL OF THE TANK SYSTEM
Taking into account the Remark 2, the linearized model is obtained by the Taylor expansion of (5.5) around the assumed equilibrium state
dh
= Jh + Ju (5.7)
Hq
dt
where: h=H-H0 is the modified state vector (deviation from the equilibrium state H0 ), u=q-q0 is deviation of the control, relative to q0, Jq, JH are Jacobians of the function (5.5):
∂
∂
F( H,q ) F( H,q )
J
J
=
=
⎢
⎥
⎢
⎥
.
H
q
∂
H
∂
q
HH HH
=
0
,q=q
0
=
0
,q=q
0
The nxn matrix JH takes the following general form for the cascade of n-tanks
⎡ ⎢ ⎢⎢
∂F1
00 K 0
∂H1 ∂F2 ∂F2
00
∂H1 ∂H2 ∂F3
⎥ ⎥⎥
MM
∂fF n
000 K
∂
Hn
∂F3
J
=
.
H
0
0
∂H2 ∂H3
H =H0
For n-tank system the Jacobian matrices are in the following form
− C1 α1
K 00
1−α1
(H ) β (H )
10 110
⎢⎢
(
C α− C α
11 22
00
1−α11−α2
) β (H )(H ) β (H )
J
H
=
H
10 2 20 20 2 20
MM
C α− C α
n−1 n−1 nn
00 K
1−α
1−α n
n−1
(H(n−1)0 ) βn (Hn0) (Hn0) βn (Hn0)
1
⎢ ⎢
⎥ ⎥
β1(H10 )
0
0
M
0
J =
q
.
The linear model can be used for the local stability analysis and for the design of local controllers of the pump-controlled system.
4.5 DEFINITIONS OF CONTROL TASKS
Under the Assumptions 1 the following example control problems can be formulated.
Pump-controlled system, open loop control
For a defined objective function find a control q(t) transferring the system from a given initial state H 0 to a given target state H f in a minimum time, while satisfying: 0< q(t ) ≤ qmax 0 ≤ H (t) ≤ H .
i i max
Example: time-optimal control [6]. Close-loop control of pump-controlled system (Fig. 4.5)
For a defined objective function find a feedback control (linear, nonlinear) q( H1 ,H2 ,H3 )stabilizing the system at the given desired state H f , while satisfying:
0 < q(t ) ≤ qx 0 ≤ H (t) ≤ H .
i i max
⎥⎥

For a defined objective function find a feedback control C ( H ),C ( H ),C ( H ), stabilizing
1122 33
Hf
the system at the given desired state , while satisfying: 0 < C (t) ≤ C
i i max
0 ≤ H (t) ≤ H .
i i max
The target (desired) state is usually selected as the steady-state (equilibrium) point of the process.
5. IDENTIFICATION
The identification of the triple tank system consist of the following steps:
- liquid level sensors characteristic curves,
- DC pump characteristic curve,
- proportional valves characteristic curves,
- identification of parameters of the mathematical model.
The identified parameters and characteristic curves are used in simulation and real-time experiments (see Section 7).
Parameters and characteristic curves given below and introduced into Simulink demo models are only examples.
Therefore, it is recommended to identify the current system parameters before starting experiments.
5.1 SENSOR CHARACTERISTIC CURVE
All three tanks are equipped with piezo-resistive pressure transducer (and the appropriate electronic interface) for measuring the level of the liquid. The pressure sensors provide a very accurate and linear frequency output — proportional to the applied pressure of liquid. The characteristic curve of the level sensor which describe liquid level versus frequency can be essential consider as linear:
Level = Gain*(Freq – freq_bias) (5.1)
The parameter of the sensor characteristic curve can be obtained by measuring the liquid level and the corresponding frequency output for at least two points and fitting the characteristic curve.
For instance, the measured levels of liquid and corresponding output frequencies of three sensors (Tank1, Tank 2 and Tank 3) are shown in Table 1.
Fig. 5.1 presents an example of approximation obtained by identification methods for Sensor 1 data is given in Table 1.
Table 1
| Level [m] | sensor 1 freq1 [Hz] | sensor 2 freq2 [Hz] | sensor 3 freq3 [Hz] |
|---|---|---|---|
| 0.05 | 2805 | 2795 | 2743 |
| 0.15 | 3507 | 3486 | 3419 |
| 0.25 | 4192 | 4177 | 4084 |
Level [m]
Sensor 1 characteristic
0.3
0.25
0.2
0.15
0.1
0.05
0
-0.05 2400 2600 2800 3000 3200 3400 3600 3800 4000 4200 Sensor output [Hz]
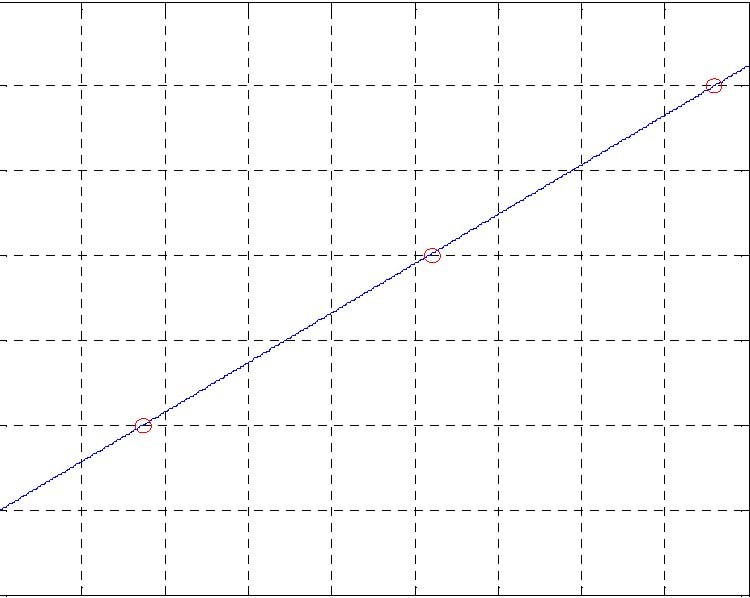
Fig. 5.1 Pressure sensor characteristic. Red points–measurements, solid line–fitting line When Table 1 is transferred to MATLAB the command polyfit(freq1,Level,1) for sensor 1 gives: a =0.00014418888640 b = -0.35485335425418 in the linear fitting equation: Level = a*Frequency +b. Comparison to equation 5.1 results: Gain_ 1 = 0. 0001441888864 and Bias_ 1 = 2461.03124248978 Similar procedure gives for sensor 2 and sensor 3 following values: Gain_2 = 0. 00014471780029 and Bias_2 = 2449.5 Gain_3 = 0. 00014913908601 and Bias_3 = 2409.56077554064. To store permanently the identified parameters the following commands must be executed:
TankScaleCoeff = [Gain_1 Gain_2 Gain_3 1 1]; TankBias=[Bias_1 Bias_2 Bias_3 0 0]; save matlabroot/toolbox/Multitank/m/TankV2PU_Coeff.m4 TankBias TankScaleCoeff -V4;
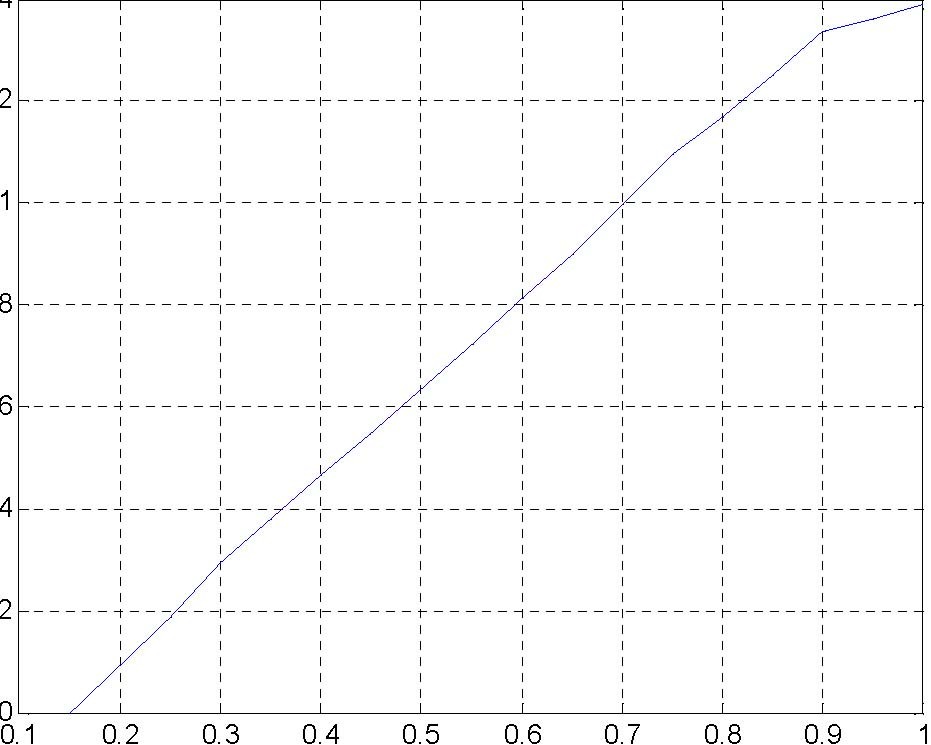
5.2 IDENTIFICATION OF VALVES
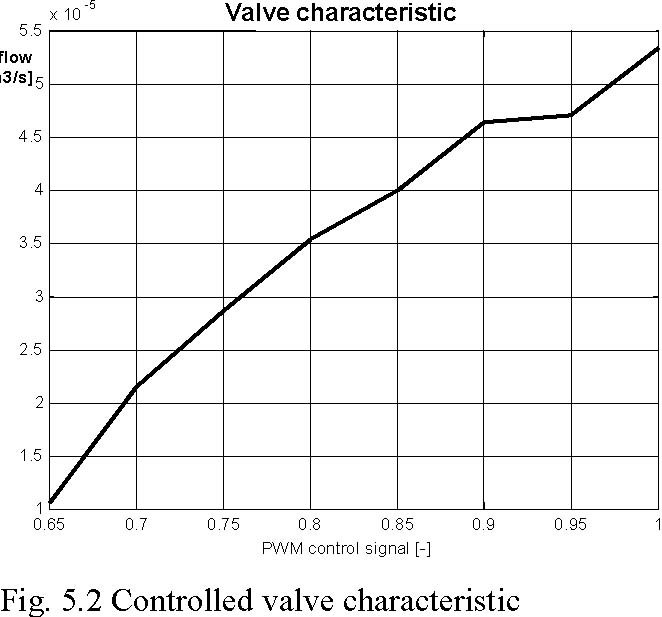
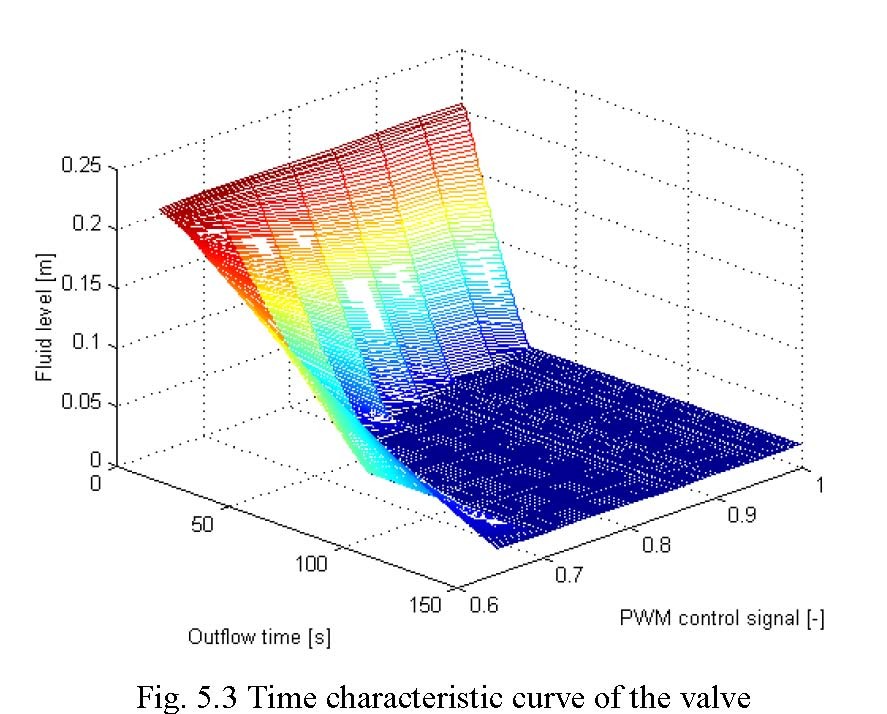
The bottom outflow of each tank is equipped with the controlled valve. The valves are adjusted using the PWM signal from the power interface. Fig. 5.2 shows characteristic curve of one of the valves. Fig. 5.3 demonstrates how the outflow depends on the level, for a given control signals.
5.5
Measured outflow [m3/s]
5
4.5 4
3.5 3
2.5 2
1.5
1 PWM control signal [-]
5.3 IDENTIFICATION OF PUMP
The system is equipped with DC pump providing liquid transportation from the lowest tank to the upper tank. The goal of the DC pump is to adjust the inflow to the upper tank according to the control signals.
The DC pump is supplied from the power interface by an appropriate PWM control signal. The frequency and pulse width of the PWM signal can be set using the PWM function from the Tank Class in MATLAB (see section 9) or by setting parameters of the DC driver in Simulink.
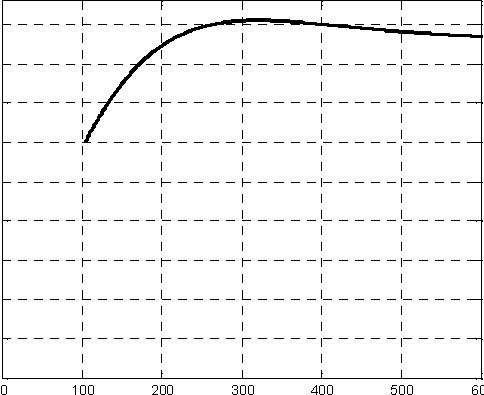
The DC pump experimental characteristic curve (Fig. 5.4) represents dependence between outflow and (in m3/s) and the pulse width value of the PWM control signal.
The inverse averaged experimental DC pump characteristic curve can be applied in the control-loop “look-up table” of LQR real-time controller example, (Section 7)
-4 Pump characteristic x 10
1.4
1.2
1
0.8
0.6
0.4
0.2
0
Control [--]
Fig. 5.4 DC pump characteristic curves measured for PWM frequency 300 Hz (PWMPrescaler=31 and 12-bit mode)
Volume [m3/s]
5.4 IDENTIFICATION OF PARAMETERS OF THE TANKS
For fixed valves settings the following parameters of the mathematical models of the tank system (Section 4) have to be identified experimentally:
Ci -resistance of the output orifice of i tank,
αi -flow coefficient for i tank, i = 1,2,3 .
For each tank the outflow experiment has been performed, the data are collected and the characteristic curves has been fitted to the data (Fig. 5.5). For this purpose FMINS procedure from MATLAB Optimization Toolbox was applied for the objective function given as
3 N
J = ∑ wk ∑( Hk(i ) − Hkm( i ))2
k =1 i=1
where: Hk(i) -are the measurements for k-tank at i-time point, Hm
k (i)-are the simulation results for k-tank, wk – is a weighting coefficient for k-tank.
Hm(0)
C1
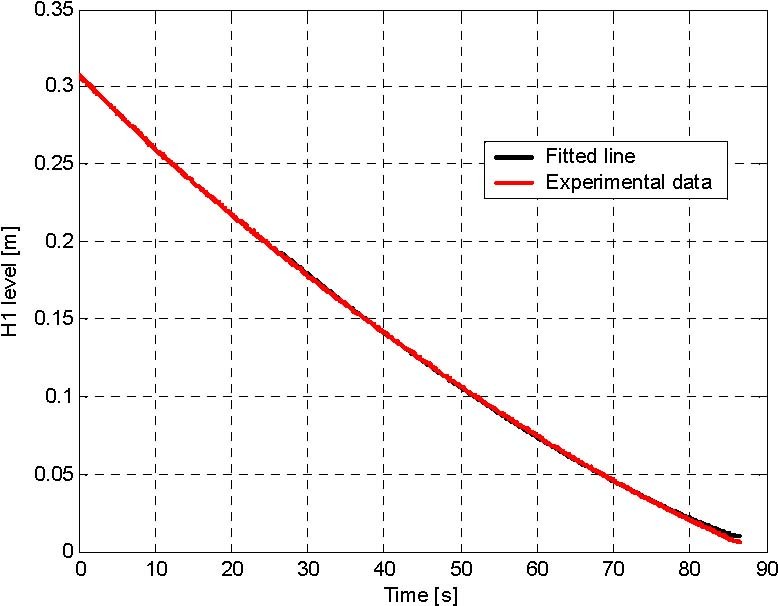
Fig. 5.6 The upper tank identification: C1 = 5.6578e-005, Alfa1 = 0.2900
C2

Fig. 5.7 The middle tank identification: C2 = 5.5800e-005, Alfa2 = 0.2256
C3
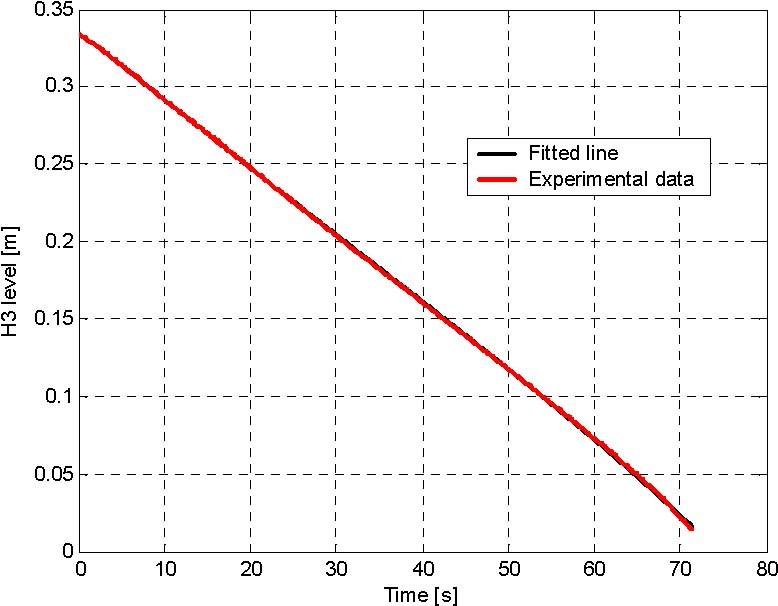
Fig. 5.8 The lower tank identification: C3 = 7.4102e-005, Alfa3 = 0.2487
6. REAL-TIME CONTROL EXPERIMENTS
In the following section a number of control experiments is described. Each experiment consists of the simulation phase and real-time phase.
The consistence of simulation and experimental results are achieved only if a proper identification procedures has been applied (including both the static and dynamic characteristic curves of the process).
6.1 DESIGN OF LINEAR CONTROLLER
The tank system demo presented in this section deals with the control task: reach and stabilize the levels in tanks at steady-state point H0 by an adjustment of the pump operation.
The steady-state points can be calculated using the formula from Section 4. The design of the continuous LQ controller is presented below. For a very small value of the sampling time the response of the discrete system converges to the response of the corresponding continuous system. It is just our case.
The linearised dynamical model of the triple tank system is described by the linear differential equations (see Section 4):
dh
= Ah + Bu , (6.1)
dt
where the matrices A and B are as follows:
⎤
A =
⎢⎢⎢⎢⎢⎢⎢⎢⎢
⎛⎜⎜⎝
wc
− C1α1
00
1−α1
awH 1
C α− C α
11 22
0
⎛
H
H
1
−α
1−
α
2 2
+
b
H
b
H
+
1 2
⎟⎟
⎟⎟
1 2
H
H
2 2
max max
22
−−
−−
(H
H
(H
H
2
⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥
3
max
32 3
max
33
H =H
where H0 is equilibrium state of the nonlinear tanks system
1
aw
⎤
⎥⎥⎥ ⎢⎢⎢
B =
0
,
0
and h=H-H0 is the modified state vector (deviation from the equilibrium state H0 ), u=q-q0 is the deviation of the control relative to from q0. A typical quadratic cost function has the form
∞
1
[hT(τ )Qh(τ ) uT(τ )Ru(τ )]dτ
J(u )
=
∫
+
(6.2)
,
2
0
where:
- Q is a nonnegative definite matrix Q ≥ 0, Q = QT ,
- R is a positive definite matrix R > 0, R = RT , in our case R is a scalar,
- The pair (A, B) is controllable.
The weighting matrices Q and R are selected by the designer but they must satisfy the above conditions. This is most easily accomplished by choosing Q to be diagonal with all diagonal elements positive or zero.
The LQR optimal scalar control u* is given then by: (6.3)
u* =−K*h
where K* is the optimal state feedback matrix.
The optimal control problem is now defined as follows: find the gain K such that the feedback law (7.3) minimizes the cost function (6.2) subject to the state equation (6.1). The optimal feedback gain can be obtained by iterative solution of the associated matrix Riccati equation:
T −1 T
SA + AS − SBR BS + Q = 0
To solve the LQ controller problem the lqry function can be used from the Matlab Control System Toolbox. The synopsis of lqry is: [K,S,E] = lqry(A,B,C,D,Q,R).
The LQ control simulations and experiments were performed for the following parameters:
- C1 = 1.0057e-004 , C2 = 1.1963e-004, C3 = 9.8008e-005. These values reffers to fully open manual valves.
- Desired levels and control values: H1,0 = 0.1425 m, H2,0 = 0.1007 m, H3,0 = 0.1500 m, and the corresponding steady-state in-flow: Q0 = 3.7958e-005 m3/s.
• The starting point: H1(0)= H2(0) = H3(0)= 0 m,
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
• The weighting matrices Q and R: Q
=
⎢⎢
⎥⎥
,
R
=
15000000
.
The optimal gain matrix K for considered parameters was calculated as
K * = [0.1983e -3 0.0765e -3 0.0496e -3].
Simulation
The LQR simulation can be performed from the Tank System Multitank Control Window by invoking LQR from the group Simulation Models. After clicking the LQR block the following window opens (Fig. 6.1).
Tank 3 LQR Controller
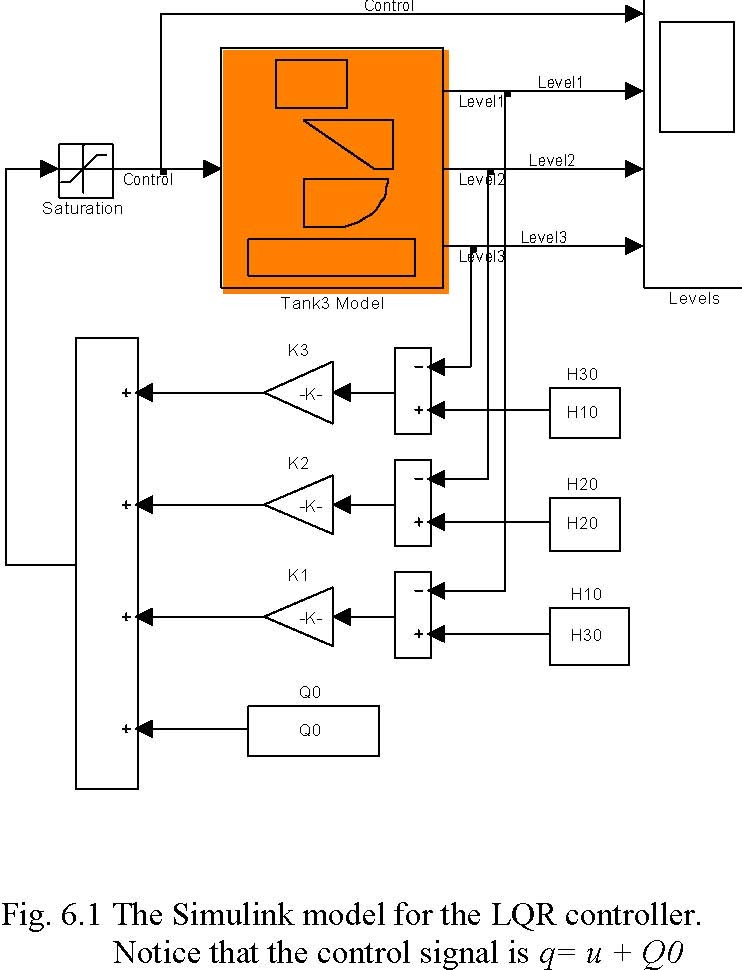
The steady-state desired value H10, H20, H30 and Q0 were introduced into constant blocks H10, H20, H30, Q0 respectively (see equation 5.6), as well as the optimal gain vector K (gain blocks K1, K2, K3). The identified parameters of the model as well as the starting point (initial conditions) can be set by double clicking the Tank Model block (Fig. 6.2).

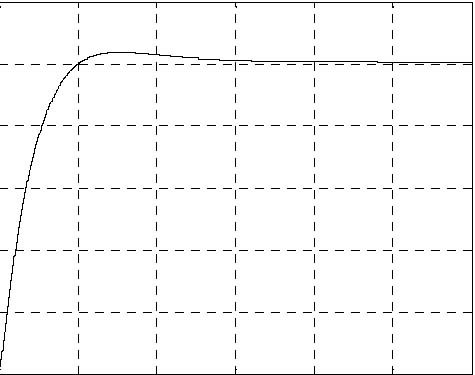
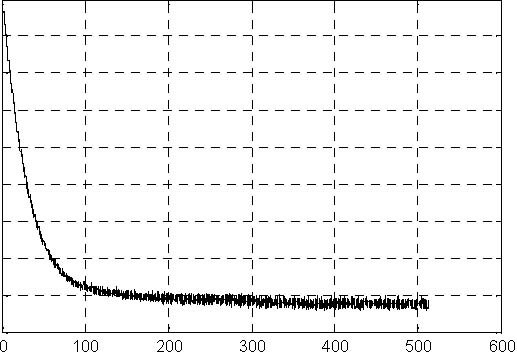
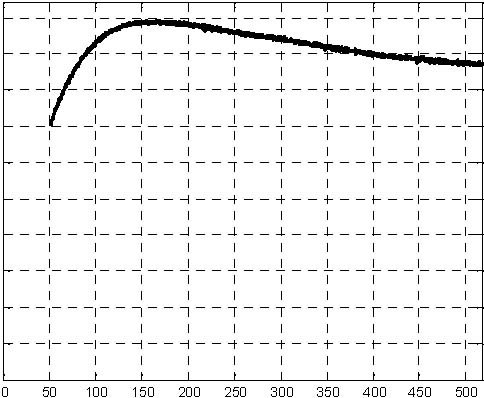
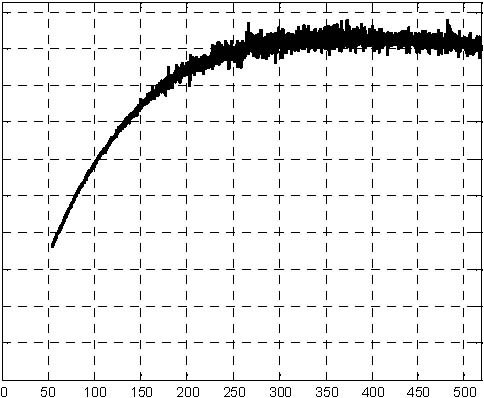
The simulation results are given in Fig. 6.3, Fig. 6.4, Fig. 6.5 and Fig. 6.6. The levels have achieved the desired value after 520 seconds approximately.
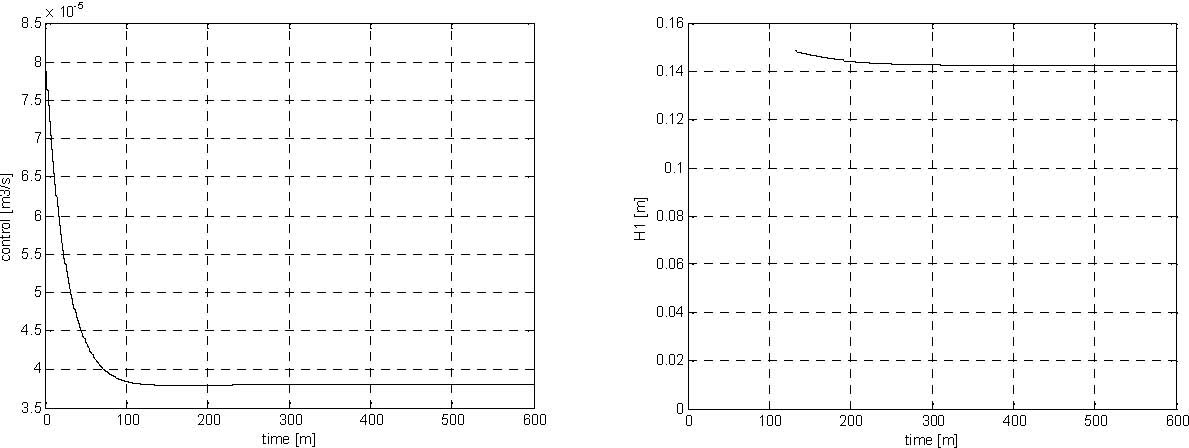
Fig. 6.3 Pump control signal (simulation) Fig. 6.4 Level H1 (simulation)
 0.04
0.04
0.02
0.02
0 0 100 200 300 400 500 600
0 0 100 200 300 400 500
time [m] time [m]
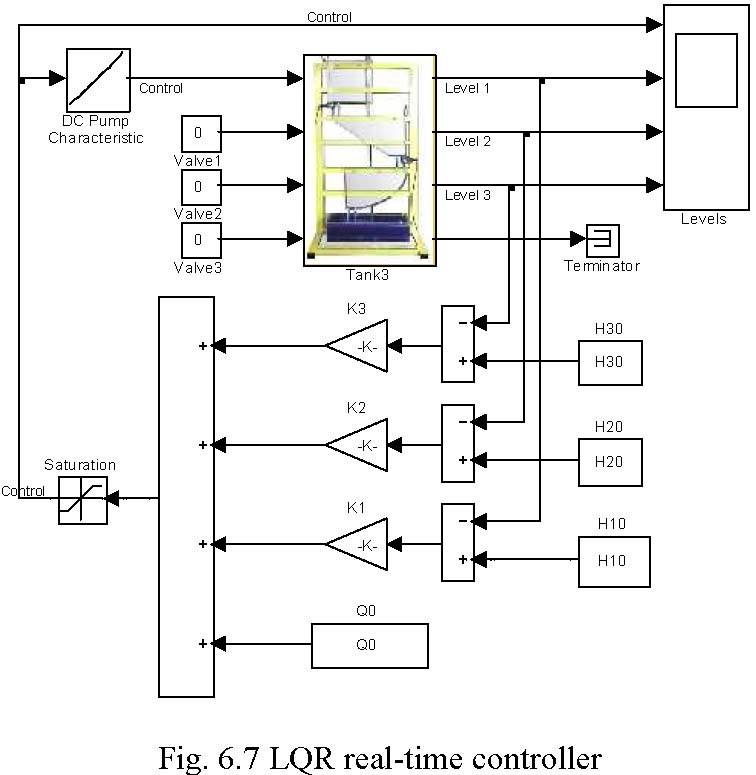
Real-time experiment
The LQ experiment can be performed from the Multitank Control Window by invoking LQR Experiment from the Demo Controllers group. After clicking on the block the following window opens (Fig. 6.7). TheTank Model block is replaced by the drivers block (see description in Section 3). The inverted characteristic curve of the pump is represented by it Look_Up Table.
Tank 3 LQR Controller
0.12
0.16
0.14
0.1
0.12
0.08
0.1
H2 [m]
H3 [m]
0.06 0.08
0.06
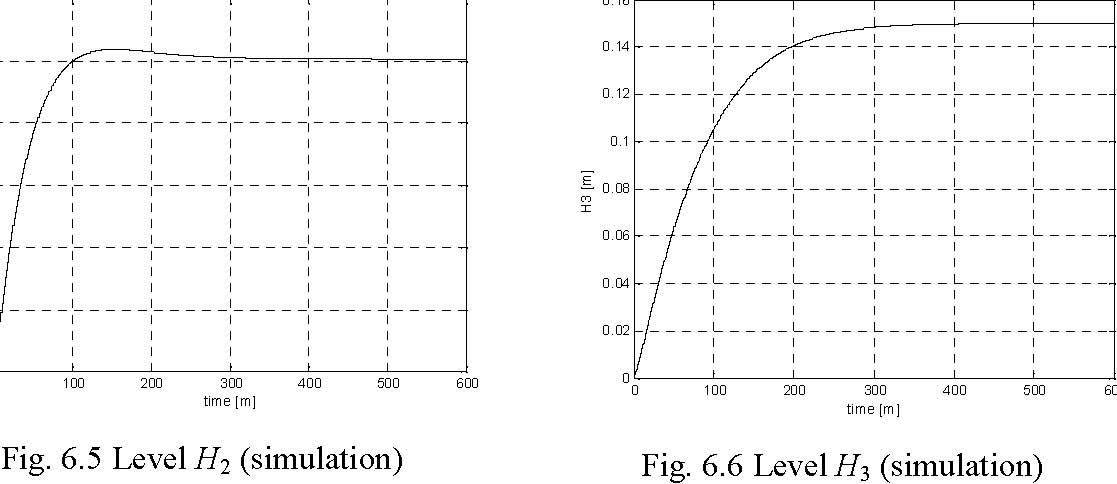
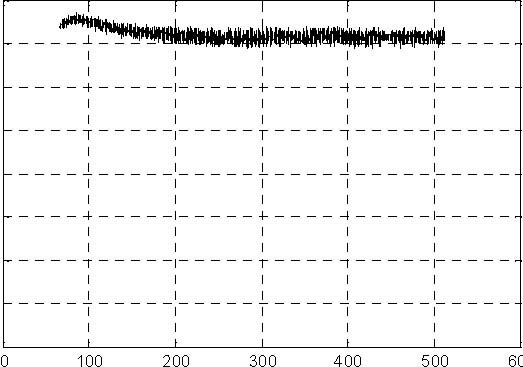
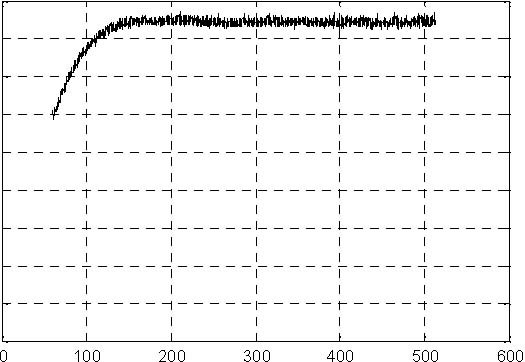
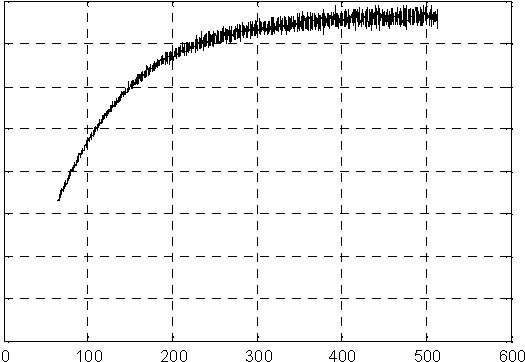
The results of experiments are given in Fig. 6.8, Fig. 6.9, Fig. 6.10 and Fig. 6.11.
x 10-5
8
0.16
7.5
0.14
7
0.12
6.5
6
5.5
5
4.5 4
3.5
time [m]
Fig. 6.8 Pump control signal
0.1
0.08
0.06
0.04
0.02 0 time [m]
Fig. 6.9 H1 level
0.16
control [m3/s]
H3 [m] H1 [m]
0.09
0.14
0.08
0.12
0.07
0.1
0.06
H1 [m]
0.08
0.05
0.06
0.04
0.04
0.03
0.02
0.02
0.01
0 time [m] time [m]
Fig. 6.10 H2 level Fig. 6.11 H3 level
6.2 FUZZY CONTROLLER
In this section we demonstrate how to develop and edit fuzzy inference systems “by hand”, using Fuzzy Toolbox from Mathworks. The following steps are essential in the design of a fuzzy controller:
- selection of input/output variables,
- scaling the variables (if necessary),
- definition of membership functions for all variables –“fuzzification”,
- development of the inference mechanism – fuzzy rules,
- selection of the “defuzzification” strategy,
- re-scaling the variables (if necessary).
INTECO
www.inteco.com.pl
There are two methods of building a fuzzy controller: interactive using the graphical tool and automatic using the clustering and adaptive neuro-fuzzy mechanism. There are also two types of fuzzy inference system: Mamdani and Sugeno. In this section we focus on the Mamdani inference system edited interactively. This approach makes possible to understand in a direct way consequences of modifications being introduced into the inference mechanism and membership functions.
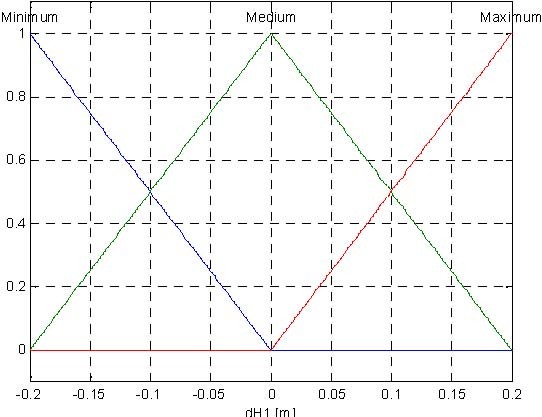
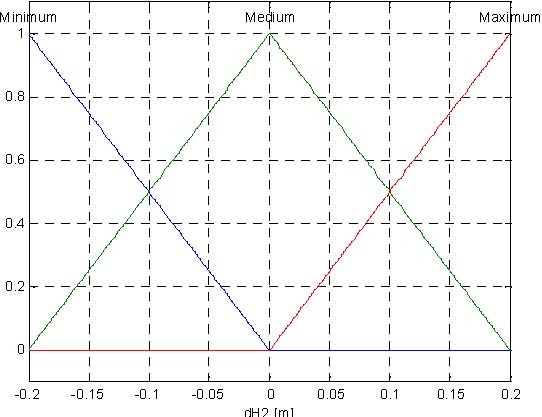
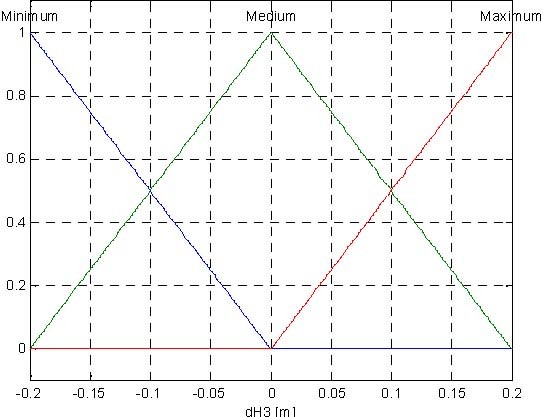
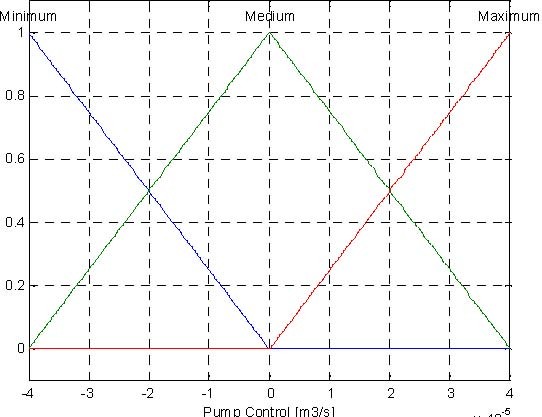
The proposed fuzzy controller for the tank system has three inputs and one output (control). The input variables are the following:
dH = H − H , dH = H − H , dH = H − H , where:
110 1 220 2 330 3
H
H
⎡
⎤
10 1
⎢
⎥
desired levels,
H
=
⎢
⎥
H
H
H
current value of levels.
=
0
20 2
H
H
30 3
The presented fuzzy controller uses Mamdami inference system. The Control Surface (Fig. 6.12) is generated with three membership function for dH1, dH2, dH3 for input signals, three membership function for control signal (Fig. 6.13) and 27 rules presented in Table. 6.1.
-5
x 10
2
Pump Control [m3/s]
1 0 -1 -2
-0.2
0
0.2
0.1
0
0.2 -0.1
-0.2
dH2 [m]
dH1 [m]
Fig. 6.12 Pump control surface versus dH1 and dH2 input signals
1
1
0.8
0.8
Degree of membership Degree of membership
Degree of membership Degree of membership
0.6 0.6
0.4 0.4
0.2
0.2
0
0
1
1
0.8
0.8
0.6 0.6
0.4 0.4
0.2
0.2
0
0
-5
x 10
Fig. 6.13 Membership function for dH1, dH2, dH3 and pump control signals
Table 6.1. Rules for fuzzy controller
| No. | Rule |
| 1 | If (dH1 is Maximum) and (dH2 is Maximum) and (dH3 is Maximum) then (Pump Control is Minimum) |
| 2 | If (dH1 is Maximum) and (dH2 is Maximum) and (dH3 is Medium) then (Pump Control is Minimum) |
| 3 | If (dH1 is Maximum) and (dH2 is Maximum) and (dH3 is Minimum) then (Pump Control is Minimum) |
| 4 | If (dH1 is Medium) and (dH2 is Medium) and (dH3 is Maximum) then (Pump Control is Medium) |
| 5 | If (dH1 is Medium) and (dH2 is Medium) and (dH3 is Medium) then (Pump Control is Medium) |
| 6 | If (dH1 is Medium) and (dH2 is Medium) and (dH3 is Minimum) then (Pump Control is Maximum) |
| 7 | If (dH1 is Minimum) and (dH2 is Minimum) and (dH3 is Maximum) then (Pump Control is Maximum) |
| 8 | If (dH1 is Minimum) and (dH2 is Minimum) and (dH3 is Medium) then (Pump Control is Maximum) |
| 9 | If (dH1 is Minimum) and (dH2 is Minimum) and (dH3 is Minimum) then (Pump Control is Maximum) |
| 10 | If (dH1 is Maximum) and (dH2 is Medium) and (dH3 is Maximum) then (Pump Control is Minimum) |
| 11 | If (dH1 is Medium) and (dH2 is Maximum) and (dH3 is Maximum) then (Pump Control is Minimum) |
| 12 | If (dH1 is Maximum) and (dH2 is Medium) and (dH3 is Medium) then (Pump Control is Minimum) |
| 13 | If (dH1 is Medium) and (dH2 is Maximum) and (dH3 is Medium) then (Pump Control is Medium) |
| 14 | If (dH1 is Maximum) and (dH2 is Medium) and (dH3 is Minimum) then (Pump Control is Medium) |
| 15 | If (dH1 is Medium) and (dH2 is Maximum) and (dH3 is Minimum) then (Pump Control is Medium) |
| 16 | If (dH1 is Minimum) and (dH2 is Medium) and (dH3 is Maximum) then (Pump Control is Maximum) |
| 17 | If (dH1 is Medium) and (dH2 is Minimum) and (dH3 is Maximum) then (Pump Control is Medium) |
| 18 | If (dH1 is Minimum) and (dH2 is Medium) and (dH3 is Medium) then (Pump Control is Maximum) |
| 19 | If (dH1 is Medium) and (dH2 is Minimum) and (dH3 is Medium) then (Pump Control is Maximum) |
| 20 | If (dH1 is Minimum) and (dH2 is Medium) and (dH3 is Minimum) then (Pump Control is Maximum) |
| 21 | If (dH1 is Medium) and (dH2 is Minimum) and (dH3 is Minimum) then (Pump Control is Maximum) |
| 22 | If (dH1 is Minimum) and (dH2 is Maximum) and (dH3 is Minimum) then (Pump Control is Medium) |
| 23 | If (dH1 is Maximum) and (dH2 is Minimum) and (dH3 is Minimum) then (Pump Control is Medium) |
| 24 | If (dH1 is Minimum) and (dH2 is Maximum) and (dH3 is Medium) then (Pump Control is Medium) |
| 25 | If (dH1 is Maximum) and (dH2 is Minimum) and (dH3 is Medium) then (Pump Control is Medium) |
| 26 | If (dH1 is Minimum) and (dH2 is Maximum) and (dH3 is Maximum) then (Pump Control is Medium) |
| 27 | If (dH1 is Maximum) and (dH2 is Minimum) and (dH3 is Maximum) then (Pump Control is Medium) |
Simulation
Simulation of the fuzzy control is performed for the following parameters:
- Desired levels and control values: H10=0.096 m, H20=0.166 m, H30=0.172 m, q0=34.33e-4 m3/s.
- The start point: H1(0)= H2(0)= H3(0)=0.0 m. Before running the simulation and experiment write in the MATLAB Command Window: >> Tank3_Fis = readfis(‘Tank3_Fis’);
The Tank3_Fis.fis file (so called FIS matrix) is loaded to the MATLAB workspace and can be used by Fuzzy Logic Controller block. The simulation model of the fuzzy controller is given in Fig. 6.14 and Fig. 6.15.
Fuzzy Controller
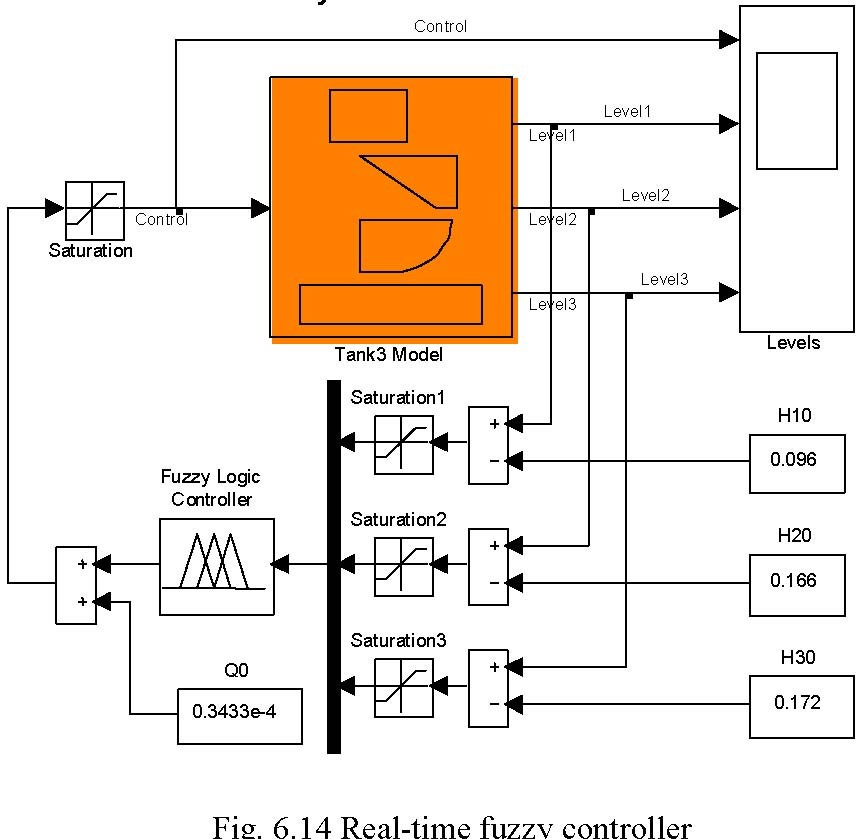
-5
x 10
10
0.16
9
0.14
8
0.12
0.1
7
5 4 Time [s]
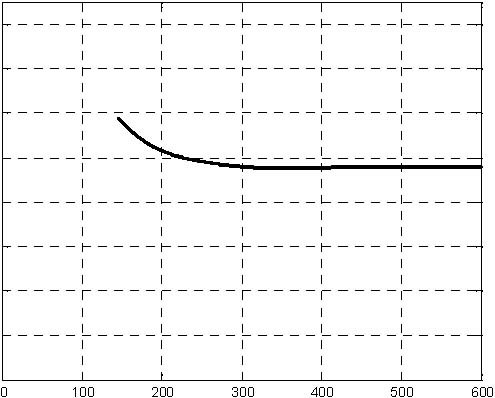
Fig. 6.16 Pump control signal

0.08
0.06
0.04
0.02 0 Time [s]
Fig. 6.17 H1 level
0.18
Pump control [m3/s]
H3 [m] H1 [m]
0.18
0.16
0.16
0.14
0.14
0.12
0.12
H2 [m]
0.1
0.08
0.08
0.06
0.06
0.04
0.04
0.02
0.02
0 0
Time [s] Time [s]
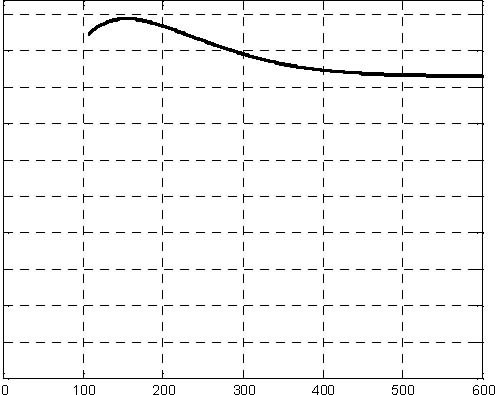
Fig. 6.18 H2 level Fig. 6.19 H3 level
Real-time Experiment
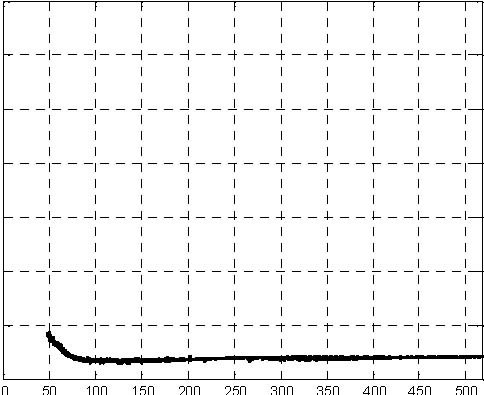
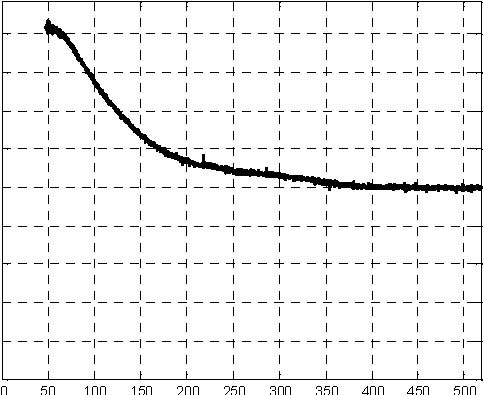
The fuzzy control experiment can be performed from the Multitank Control Window by invoking Fuzzy from the Demo Controllers group. In the model of the control system (Fig. 6.20) the Tank Model block was replaced by the driver block.
Before running experiment the FIS matrix must be loaded using following command in MATLAB Workspace:
Tank3_Fis=readfis( Tank3_Fis );
Tank 3 Fuzzy Controller
-5
x 10
10
0.18
9
0.16
8
0.14
Pump control [m3/s]
0.12
H1 [m]
0.1
0.08
0.06
0.04
0.02
0 Time [s] Time [s]
Pump control signal H1 level
INTECO
www.inteco.com.pl
0.2
0.18
0.16
0.14
0.12 0.2
0.18
0.16
0.14
0.12
H2 [m]
H3 [m]
0.1
0.08
0.08
0.06
0.06
0.04
0.04
0.02
0.02
0
0 Time [s] Time [s]
H2 level H3 level Fig. 6.21 Results of fuzzy control experiment
Multitank System -User’s Manual
7. PROTOTYPING AN OWN CONTROLLER IN RT-CON ENVIRONMENT
In this section the process of building your own control system is described. The RT-CON toolbox is used. An example how to use the MultiTank software is shown later in section 5.3. In this section we give indications how to proceed in the real-time environment.
Before starting, test your MATLAB configuration and compiler installation by building and running an example of a real-time application. MT toolbox includes the real-time model of PC speaker.
The model pc_speaker_xxx.mdl does not have any I/O blocks so that you can run this model regardless of the I/O boards in your computer. Running this model will test the installation by running Real-Time Workshop, and your third-party C compiler.
In the MATLAB command window, type
pc_speaker_vc (if you are using Visual C++ compiler)
or
• pc_speaker_watc (if you are using OpenWatcom 1.3 compiler)
Build and run this real-time model as follows:
• From the Tools menu, point to Real-Time Workshop, and then click Build Model.
The MATLAB command window displays the following messages.
### Starting Real-Time Workshop build procedure for model: pc_speaker_vc ### Generating code into build directory: C:\apps\MATLAB\R2006a\work\
pc_speaker_vc_RTCON ### Invoking Target Language Compiler on pc_speaker_vc.rtw. . . . .. . . ### Created RT-CON executable: pc_speaker_vc.dll
### Successful completion of Real-Time Workshop build procedure for model: pc_speaker_vc
• From the Simulation menu, click External, and then click Connect to target.
The MATLAB command window displays the following message. Model pc_speaker_vc loaded
• From Simulation menu, click Start real-time code.
The Dual scope window displays the output signals and you hear the speaker sound.
Only correct configuration of the MATLAB, Simulink, RTW and C compiler guaranties the proper operation of the MT system.
To build the system that operates in the real-time mode the user has to:
- create a Simulink model of the control system which consists of the Tank Device Driver and other blocks chosen from the Simulink library,
- build the executable file under RTWT (see the pop-up menus in Fig. 7.1)
- start the real-time code to run from the Simulation/Connect to target and the Simulation/Start real-time code pull-down menus.

7.1 CREATING A MODEL
The simplest way to create a Simulink model for the tank system is to use one of the models included in the Multitank Control Window as a template. For example, the Tank3_Relay can be saved as the MySystem.mdlSimulink diagram. The MySystem Simulink model is shown in Fig. 7.2 .
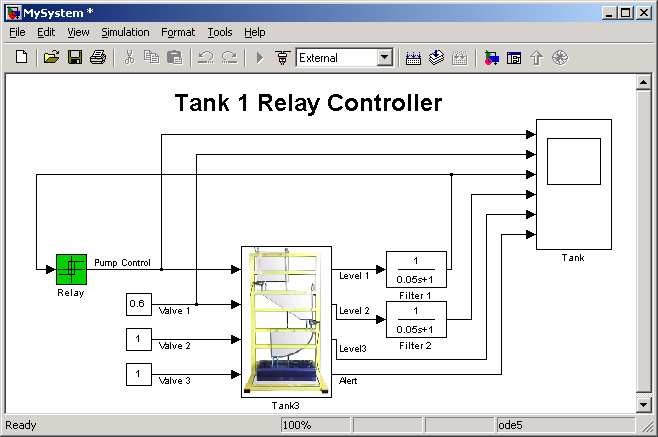
Now, you can modify the model. You have absolute freedom to develop your own controller. Remember, not to delete the Tank3 driver model. This is necessary to support the data communication with the PCI I/O board.
Though it is not obligatory, we recommend you to leave the scope (Tank block in Fig. 7.2). You need a scope to watch how the system runs. Other blocks in the window are not necessary for a new project.
Creating your own model on the basis of the old example ensures that all internal options of the model are set properly. These options are required to proceed with compiling and linking in a proper way. To put the TankDevice Driver into the real-time code a special makefile is required. This file is included to the Tank software.
You can use the most of the blocks from the Simulink library. However, some of them can not be used (see MathWorks references manual for details).
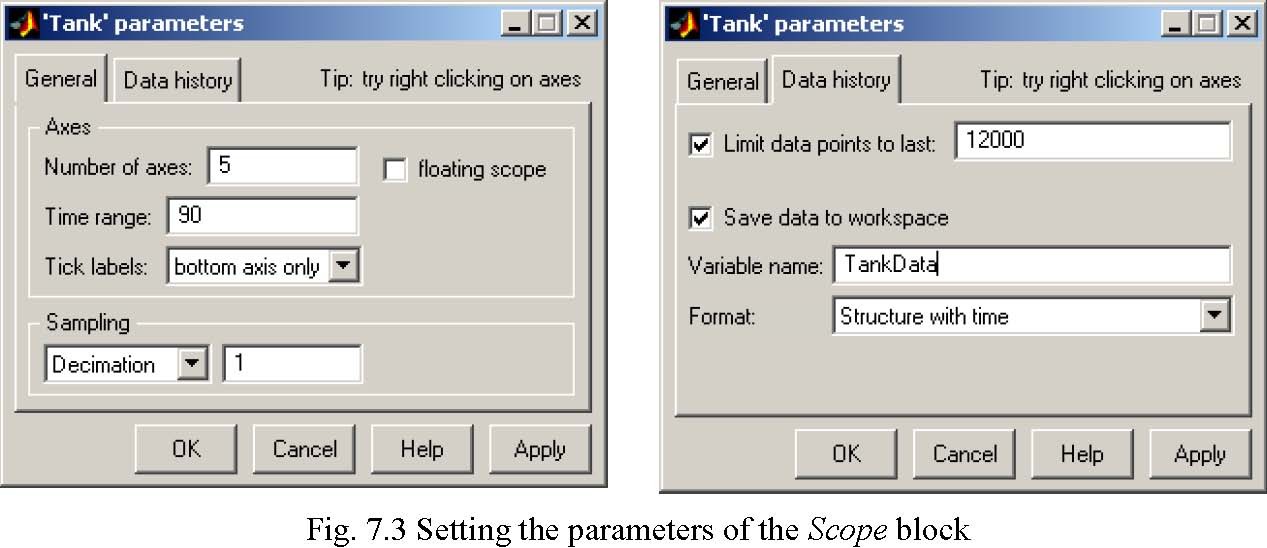
The scope block properties are important for appropriate data acquisition and watching how the system runs. The Scope block properties are defined in the Scope property window (see Fig. 7.3). This window opens after the selection of the Scope/Properties tab. You can gather measurement data to the Matlab Workspace marking the Save data to workspace checkbox. The data is placed under Variable name. The variable format can be set as structure or matrix. The default Sampling Decimation parameter value is set to 1. This means that each measured point is plotted and saved. Often we choose the Decimation parameter value equal to 5 or 10. It is a good choice to get enough points to describe the signal behaviour and to save the computer memory.
When the Simulink model is ready, click the Tools/External Mode Control Panel option and click the Signal Triggering button. The window given in Fig. 7.4 opens. Select XT Scope, set Source as manual, set Durationequal to the number of samples you intend to collect, and finally close the window.
7.2 CODE GENERATION AND BUILD PROCESS
Once a model of the system has been created the code for the real-time mode can be generated, compiled, linked and downloaded into the target processor.
The code is generated by the use of Target Language Compiler (TLC) (see description of the Simulink Target Language). The makefile is used to build and download object files to the target hardware automatically.
First, you have to specify the simulation parameters of your Simulink model in the Simulation parameters dialog box . The Real Time Workshop tab (Fig. 7.5) contains critical parameters.
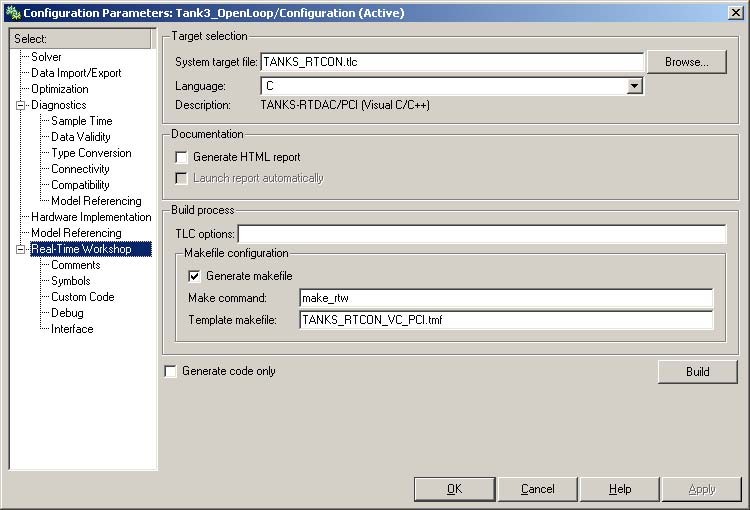
The system target file name is TANKS_RTCON.tlc. It manages the code generation process. The TANKS_RTCON_VC_PCI.TMF template makefile is responsible for C code generation using the Visual C/C++ compiler. If the Open Watcom 1.3 compiler is used the template makefile is TANKS_RTCON_WATC_PCI.TMF.
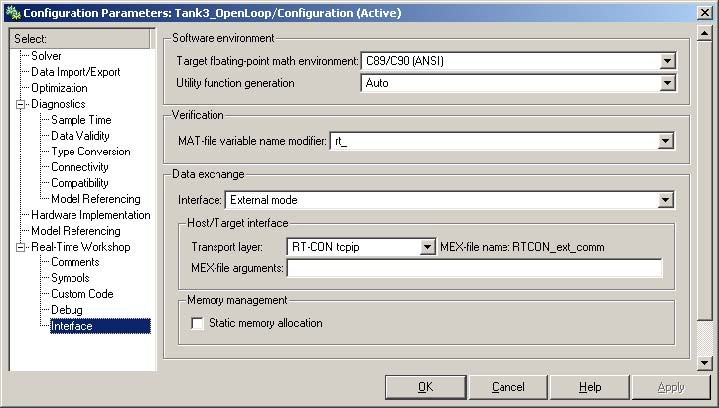
The external mode has to be set for real-time experiment. It can be done in the Real Time Workshop/Interface tab as is shown in Fig. 7.6.
The Solver tab allows you to set the simulation parameters (see Fig. 7.7). Several parameters and options are available in the window. The Fixed-step size editable text box is set to 0.01 (this is the sampling period in seconds).
The Fixed-step solver is obligatory for real-time applications. If you use an arbitrary block from the discrete Simulink library or a block from the drivers’ library remember, that different sampling periods must have a common divider.
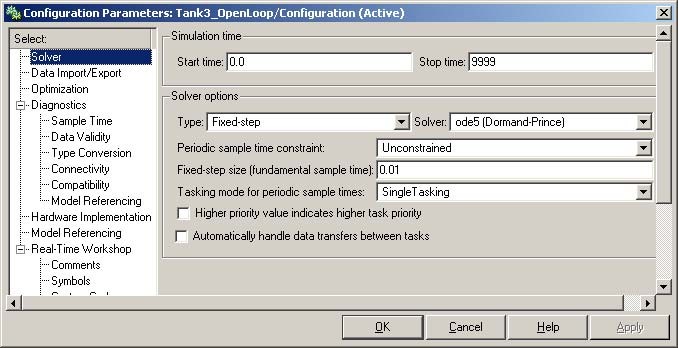
The Start time has to be set to 0. The solver method has to be selected. In our example the fifth-order integration method − ode5 is chosen. The Stop time field defines the length of the experiment. This value may be set to a large number. Each experiment can be terminated by pressing the Stop real-time code button.
If all the parameters are set properly you can start the real-time executable building process. For this purpose press the Build push button at the Real Time Workshop tag (or simply “CRTL + B”. Successful compilation and linking processes generate the following message:
Model MyModel.rtd successfully created
### Successful completion of Real-Time Workshop build procedure for model: MyModel
Otherwise, an error message is displayed in the MATLAB Command Window.
In this case check again your MATLAB configuration and simulation parameters.
8. DESCRIPTION OF THE TANK CLASS PROPERTIES
The Tank is a MATLAB class, which gives the access to all the features of the RT-DAC/PCI board equipped with the logic for the tank model. The RT-DAC/PCI board is an interface between the control software executed by a PC computer and the power-interface of the multitank system. The board contains the following blocks:
- PWM generation block – the FPGA logic generates up to six signals. The PWM prescaler for each PWM block determines the frequency of the corresponding PWM wave. The PWM waves control up to five valves and the pump. The default prescaler value is 31 which is equivalent to the PWM wave frequency equal to 305Hz. This frequency is recommended for the valves and for the pump. The PWM blocks can operate in two modes: 8-bit resolution and 12-bit resolution. The 12-bit mode is selected as the default one. In the 12-bit mode a single PWM period contains 4095 impulses of the output prescaler frequency. The time of logic output ‘1’ is set by a number from 0 to 4095. In the 8-bit mode a PWM period contains 255 impulses of the output prescaler frequency. The time of logic ‘1’ is set by a number from 0 to 255. The 8-bit mode is used for high speed. The 12-bit mode gives a high accuracy,
- Digital inputs are responsible for reading the signals from frequency sensors of a liquid levels. The input is proportional to the liquid level. The Tank class converts the value read from the D input to the level expressed in meters.
All the parameters and measured variables from the RT-DAC/PCI board are accessible by the appropriate methods of the Tank class. The object of the Tank class is created by the command:
object_name = tank;
The get method is called to read a value of the property of the object:
property_value = get( object_name, ‘property_name’ );
The set method is called to set new value of the given property:
set( object_name, ‘property_name’, new_property_value );
The display method is applied to display the property values when the object_name is entered in the MATLAB command window.
This section describes all the properties of the Tank class. The description consists of the following fields:
| Purpose | Provides short description of the property |
| Synopsis | Shows the format of the method calls |
| Description | Describes what the property does |
| Arguments | Describes arguments of the set method |
| See | Refers to other related properties |
| Examples | Provides examples how the property can be used |
8.1 BASEADDRESS
Purpose: Read the base address of the RT-DAC/PCI board.
Synopsis: BaseAddress = get( TankObj, ‘BaseAddress’ );
Description: The base address of RT-DAC/PCI board is determined by operating system. Each Tank object has to know the base address of the board. When a Tank object is created the base address is detected automatically. The detection procedure detects the base address of the first RT-DAC/PCI board plugged into the PCI slots.
Example: Create the Tank object:
TankObj = tank;
Display its properties by typing the command:
TankObj
| Type: | Tank Object | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BaseAddress: | 54272 / D400Hex | ||||||||||||
| Bitstream ver.: | x202 | ||||||||||||
| PWM: | [ 4095 | 0 | 4095 | 4095 | 0 | 0 ] | |||||||
| PWMPrescaler: | [ 1 | 31 | 31 | 31 | 31 | 31 ] | |||||||
| PWMMode: | [ 1 | 1 | 1 | 1 | 1 | 1 ] | |||||||
| Valve: | [ 1 | 1 | 0 | 0 | 0 ] | ||||||||
| Pump: | [ 1 ] | ||||||||||||
| Scaling coeff.: | [ 0.0001 0.0001 0.0002 1.000 1.000 ] | ||||||||||||
Zero level bias: [ 0.002 0.002 0.002 0.000 0.000 ] Frequency: [ 2430 4746 3143 0.000 0.000 ] [Hz]
| Level: | [ 0.029 | 0.238 | 0.171 | 0.000 | 0.000 ] [m] | ||||
|---|---|---|---|---|---|---|---|---|---|
| Safety max.: | [ 0.306 | 0.306 | 0.306 | 0.306 | 0.306 ] [m] | ||||
| Safety min.: | [ 0.297 | 0.297 | 0.297 | 0.297 | 0.297 ] [m] | ||||
| Safety flag: | [ 1 | 1 | 1 | 1 | 1 ] | ||||
| Safety alert: | [ 1 ] | ||||||||
| Read the base address: | |||||||||
BA = get( TankObj, ‘BaseAddress’ );
8.2 BIAS
Purpose: The bias level of the liquid level measurements. The bias values are equal to the levels read from the A/D converters when the tanks are empty. When a new value of this property is set the new biases are stored in a file for future use.
Synopsis: B = get( TankObj, ‘Bias’ );
set( TankObj, ‘Bias’, NewBias );
Description: The bias value is subtracted from value obtained from the A/D converter to obtain the bias-less level value.
See: ScaleCoeff
Examples: see Section 3.2
8.3 BITSTREAMVERSION
Purpose: Read the version of the logic design for the RT-DAC/PCI board.
Synopsis: Version = get( TankObj, ‘BitstreamVersion’ );
Description: This property determines the version of the logic design of the RT-DAC/PCI board. The tank systems may be different and the detection of the logic design version makes it possible to check if the logic design is compatible with the physical model.
8.4 PWM
Purpose: Set and get the duty cycle of the PWM waves.
Synopsis: PWM = get( TankObj, ‘PWM’ );
set( TankObj, ‘PWM’, NewPWM );
Description: The property determines the duty cycle of the PWM waves for the valves and for the pump. The first PWM channel is responsible for the pump control. The remaining five channels are applied to control the valves. The NewPWM variable is a 1x6 vector. Each element of these vectors determines the parameters of the single PWM wave. The values of the elements of this vector can vary from 0 to 255 if the 8-bit mode is used, and from 0 to 4095 if the 12-bit mode is selected. The value 0.0 means the zero control and the maximum means the maximum control.
The values of the PWM property are equivalent to the internal RT-DAC/PCI board values. The most convenient way to control the pump and the valves if use the Valves and the Pumpproperties.
Example: set( TankObj, ‘PWM’, [ 1024 1024 2048 0 0 ] );
See: Pump, Valve, PWMPrescaler, PWMMode
8.5 PWMPRESCALER
Purpose: Determine the frequency of the PWM waves.
Synopsis: Prescaler = get( TankObj, ‘PWMPrescaler’ );
set( TankObj, ‘PWMPrescaler’, NewPrescaler );
Description: The input frequency for the PWM channels is equal to 40MHz. This frequency is divided by the counter (called prescaler), which creates the PWM base period. The NewPrescaler variable is a 1x6 vector. Each element of these vectors determines the parameters of the single PWM wave frequency. The valid prescaler values are numbers from 0 to 65535. The frequency of the PWM wave is calculated from the formula:
fxtal
f = for 8-bit mode,
PWM ( prescaler +1) ∗255
fPWM = fxtal for 12-bit mode. ( prescaler +1) ∗4095
The recommended working conditions of the pump and the valves require that the PWM waves frequency is approximately equal to 300Hz. In the 12-bit operating mode this frequency corresponds to the prescaler value 31 and should not be changed.
See: PWM, PWMMode
Example: To set the prescaler value equal to 31 for all the PWM channels execute the command:
set( TankObj, ‘PWMPrescaler’, [ 31 31 31 31 31 ] );
8.6 PWMMODE
Purpose: Determines the 8-bit or 12-bit PWM mode.
Synopsis: Mode = get(TankObj, ‘PWMMode’ );
set( TankObj, ‘PWMMode’, NewMode );
Description: The PWM blocks can operate in two modes: 8-bit resolution and 12-bit resolution. The 12-bit mode is selected as the default one. In the 12-bit mode a single PWM period contains 4095 impulses. The time of logic output ‘1’ is set by a number from 0 to 4095. In the 8-bit mode a PWM period contains 255 impulses. The time of logic ‘1’ is set by a number from 0 to 255. The 8bit mode is used for high speed. The 12-bit mode gives a high accuracy and is selected as the default mode for all the tank experiments.
The NewMode variable is a 1x6 vector. Each element of these vectors determines the operating mode of the single PWM wave. The value of 0 selects the 8-bit mode and the value of 1 selects the 12-bit mode.
See: PWM, PWMPrescaler
Example: To set the 12-bit PWM generation mode execute the command:
set( TankObj, ‘PWMMode’, [ 1 1 1 1 1 ] );
8.7 VALVE
Purpose: Set and get the control value for the valves.
Synopsis: PWM = get( TankObj, ‘Valve’ );
set( TankObj, ‘Valve’, NewValveControl );
Description: The property determines the control value for the valves. The NewValveControl variable is a 1x5 vector. Each element of these vectors determines the control for a single valve starting from the upper tank. The values of the elements of this vector can vary from 0.0 to 1.0. The value of
0.0 means the zero control and the vale of 1.0 means the maximum control. If the control is equal to 0.0 the valve is closed. If it is equal to 1.0 the valve is fully opened.
See: Pump, PWM
Example: To open only the upright valve execute the following command:
set( TankObj, ‘Valve’, [ 1 0 0 0 0 ] );
8.8 PUMP
Purpose: Set and get the control value for the pump.
Synopsis: PWM = get( TankObj, ‘Pump’ );
set( TankObj, ‘Valve’, NewPumpControl );
Description: The property determines the control value for the pump. The NewPumpControl variable is a scalar. Its value can vary from 0.0 to 1.0. The 0.0 value means the zero control and the 1.0 value means the maximum control. If the control is equal to 0.0 the pump is stopped. If it is equal to 1.0 the outflow from the pump is the maximum.
See: Valve, PWM
Example: To establish the 0.5 value control to the pump execute the following command:
set( TankObj, ‘Pump’, 0.5 );
8.9 SCALECOEFF
Purpose: Return and set the scaling coefficient of the liquid level measurements. When a new value of this property is set the new scaling coefficients are stored in a file for future use.
Synopsis: SC = get( TankObj, ‘ScaleCoeff’ );
set( TankObj, ‘ScaleCoeff’, NewScaleCoeff );
Description: The values obtained from the A/D converter are multiplied by the scale coefficients to obtain the levels expressed in meters.
See: Bias
Example: See Section 3.2
8.10 TIME
Purpose: Return time information.
Synopsis: T = get( TankObj, ‘Time’ );
Description: The Tank object contains the time counter. When a Tank object is created the time counter is set to zero. Each reference to the Time property updates their value. The value is equal to the number of milliseconds past since the object was created.
8.11 SAFETYFLAG
Purpose: Return the safety level flags.
Synopsis: SLF = get( TankObj, ‘SafetyFlag’ );
Description: The I/O board applied to control the multi-tank system processes the liquid level measurements to avoid the overflow. For each tank maximum and minimum liquid level is defined that turns on and off the safety alert flag. If a safety flag is active the level in the appropriate tank influences the safety alert. When the level in a safety-active tank exceeds the maximum level the pump and the automatic valves are turned off. The control is set by the I/O board to zero regardless of the control value sent out from the MATLAB/Simulink environment. The system returns to the normal operating mode if all levels in safety-active tanks fall under the minimum level. Such a safety algorithm allows to avoid the liquid overflow only in the case when the manual valves are closed. If they are not closed the overflow may occur.
This property returns five safety flags.
See: SafetyMax, SafetyMin, SafetyAlert
8.12 SAFETYMAX
Purpose: Return the maximum allowed liquid level.
Synopsis: SLF = get(TankObj, ‘SafetyMax’ );
Description: When the level in a safety-active tank exceeds the maximum level, the pump and the automatic valves are turned off. The control is set by the I/O board to zero regardless of the control value sent out from the MATLAB/Simulink environment. The system returns to the normal operating mode if all levels in safety-active tanks go below the minimum level.
This property returns five maximum levels.
See: SafetyFlag, SafetyMin, SafetyAlert
8.13 SAFETYMIN
Purpose: Return the minimum liquid level that deactivates the safety alert.
Synopsis: SLF = get( TankObj, ‘SafetyMin’ );
Description: When the safety alert flag is activated the system returns to the normal operating mode if all levels in safety-active tanks fall under the minimum level.
This property returns five minimum levels.
See: SafetyFlag, SafetyMax, SafetyAlert
8.14 SAFETYALERT
Purpose: Return the safety alert flag.
Synopsis: SLF = get( TankObj, ‘SafetyAlert’ );
Description: When the level in a safety-active tank exceeds the maximum level the pump and the automatic valves are turned off. Such conditions trigger the safety alert flag as well. The control is set by the I/O board to zero regardless of the control value sent out from the MATLAB/Simulink environment. The system returns to the normal operating mode (the safety alert flag is inactive) if all levels in safety-active tanks go below the minimum level.
This property returns 0 value for inactive safety alert flag and 1 value otherwise.
See: SafetyFlag, SafetyMin, SafetyMax
8.15 THE TANK CLASS QUICK REFERENCE TABLE
| Property Name | Description |
| BaseAddress | Read the base address of the RT-DAC/PCI board |
| BitstreamVersion | Read the version of the logic design of the RT-DAC/PCI board |
| PWM | Duty cycle of the PWM channels |
| PWMPrescaler | Prescaler values of the PWM channels |
| PWMMode | Mode of the PWM channels |
| Valve | Control values of the valves |
| Pump | Control value of the pump |
| ScaleCoeff | Frequency -to-level scaling coefficients |
| Bias | Frequency bias levels |
| SafetyFlag | Safety function flags for the tanks |
| SafetyMax | Maximum safety function levels |
| SafetyMin | Minimum safety function levels |
| SafetyAlert | Safety alert flag |
| Time | Return time information |
9. REFERENCES
[1] Graebe S.F., Goodwin G.C., Control Design and Implementation in Continuous Steel Casting, IEEE Control Systems, August 1995, pp. 64-71
[2] Cheung Tak-Fal, Luyben W.L., Liquid Level Control in Single Tanks and Cascade of Tanks with Proportional-Only and Proportional-Integral Feedback Controllers, Ind. Eng. Chem. Fundamentals, vol. 18, No. 1, 1979, pp. 15-21.
[3] Heckenthaler T., Engell S., Approximately Time-Optimal Fuzzy Control of a Two-Tank System, IEEE Control Systems, pp.24-30, 1994.
[4] Galichet S., Foulloy L., Fuzzy Logic Control of a Floating Level in a Refinery Tank, Proc. Of 3rd IEEE Int. Conference on Fuzzy Systems, Orlando, June 1994, pp. 1538-1542.
[5] Street R. L., Watters G. Z., Vennard J. K., Elementary Fluid Mechanics, John Wiley&Sons Inc., 1996.
[6] Grega W., Heterogeneous Control Laws in Open Architecture Enviroment, Third International Symposium on Methods and Models in Automation and Robotics, Międzyzdroje, Poland, September, 1996, pp. 1097-1102.
[7] Rosol M., Control of Nonlinear Liquid Flow Process, PhD Thesis – in Polish, (Grega W. supervisor), AGH University of Science and Technology, Department of Control, Krakow, 2001
url: http://www.51lm.cn/p/templates/cn/show.php?cid=0&aid=3293


