servo_um
型号: PXF3299
Modular Servo System
(MSS)
MATLAB 7 (R14 SP2/SP3) MATLAB R2006a, R2006b PCI version
User’s Manual


www.inteco.com.pl
COPYRIGHT NOTICE
© Inteco Sp. z o.o.
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior permission of Inteco Sp. z o.o.
ACKNOWLEDGEMENTS
Inteco acknowledges all trademarks. MICROSOFT, WINDOWS 98/2000/NT/XP are registered trademarks of Microsoft Corporation. MATLAB, Simulink, RTWT and RTW are registered trademarks of Mathworks Inc.
Contents
1. INTRODUCTION AND GENERAL DESCRIPTION ............................................................................ 5
1.1. Product overview................................................................................................................................... 5
1.2. Equipment and requirements ................................................................................................................. 6
1.3. Hardware installation............................................................................................................................. 7
1.4. Software installation .............................................................................................................................. 7
2. STARTING, TESTING AND STOPPING PROCEDURES ................................................................... 8
2.1. Starting procedure.................................................................................................................................. 8
2.2. Testing and troubleshooting.................................................................................................................. 8
3. SERVO CONTROL WINDOW............................................................................................................... 13
3.1. Basic test.............................................................................................................................................. 13
3.2. Manual setup........................................................................................................................................ 13
3.3. RTWT Driver ...................................................................................................................................... 17
3.4. Simulation Models............................................................................................................................... 18
3.5. Identification........................................................................................................................................ 20
3.6. Demo Controllers................................................................................................................................. 20
4. MATHEMATICAL MODEL OF THE SERVO SYSTEM................................................................... 22
4.1. Linear Model ....................................................................................................................................... 22
4.2. Nonlinear model .................................................................................................................................. 24
5. RTWT MODEL......................................................................................................................................... 26
5.1. Creating a model.................................................................................................................................. 26
5.2. Code generation and the build process ................................................................................................ 28
6. BASIC ASSIGNMENTS........................................................................................................................... 31
6.1. Basic measurements............................................................................................................................. 31
6.2. Steady state characteristics of the DC servo ........................................................................................ 33
6.3. Time domain identification.................................................................................................................. 35
6.3.1. Identification task by the surface method..................................................................................... 35
6.3.2. Time domain identification experiment........................................................................................ 36
7. ADVANCED ASSIGNMENTS ................................................................................................................ 38
7.1. PID position control............................................................................................................................. 38
7.2. PID Velocity control............................................................................................................................ 49
7.3. Multivariable control design............................................................................................................... 52
7.3.1. Pole-placement method................................................................................................................ 52
7.3.2. Deadbeat controller..................................................................................................................... 55
7.4. Optimal design method: LQ controller................................................................................................ 59
7.4.1. The continuous case..................................................................................................................... 60
7.4.2. The discrete case.......................................................................................................................... 64
8. DESCRIPTION OF THE MODULAR SERVO CLASS PROPERTIES............................................. 67
8.1. BaseAddress ........................................................................................................................................ 68
8.2. BitstreamVersion ................................................................................................................................. 68
8.3. Encoder................................................................................................................................................ 68
8.4. Angle ................................................................................................................................................... 69
8.5. AngleScaleCoeff.................................................................................................................................. 69
8.6. PWM.................................................................................................................................................... 69
8.7. PWMPrescaler..................................................................................................................................... 70
8.8. Stop...................................................................................................................................................... 70
8.9. ResetEncoder....................................................................................................................................... 70
8.10. Voltage............................................................................................................................................... 71
8.11. Therm ................................................................................................................................................ 71
8.12. ThermFlag ......................................................................................................................................... 71
8.13. Time................................................................................................................................................... 72
8.14. Quick reference table......................................................................................................................... 72
- CServo Example ................................................................................................................................ 72
- SOME TECHNICAL DATA.................................................................................................................... 76
Modular Servo System
1. Introduction and general description
The Modular Servo System (MSS) consists of the Inteco digital servomechanism and open-architecture software environment for real-time control experiments. The main concept of the Modular Servo System was to create a rapid and direct path from control system design to hardware implementation. The Modular Servo System supports the real-time design and implementation of advanced control methods, using MATLAB® and Simulink® tools, and extends the MATLAB environment in the solution of digital servomechanism control problems.
The integrated software supports all phases of a control system development:
• on-line process identification,
- control system modelling, design and simulation,
- real-time implementation of control algorithms.
The Modular Servo System uses standard PC hardware platforms and Microsoft Windows operating systems. Besides the hardware and the related software you obtain the User’s manual. The manual:
- shows step-by-step how to design and generate your own real-time controller in MATLAB/Simulink environment,
- contains the library of ready-to use real-time controllers,
- includes the set of preprogrammed experiments.
1.1. Product overview
The MSS setup (Fig. 1.1) consists of a several modules mounted at the metal rail and coupled with a small clutches. The modules are arranged in the chain. At the beginning of the chain must be placed DC motor with tachogenerator module and at the end the chain the gearbox with the output disk must be located. The DC motor drives in turn modules as follows: inertia, magnetic brake, backlash and gearbox with output disk. The angle of rotation of the DC motor shaft is measured using an incremental encoder. The encoder can be placed between any modules where you want to measure the angle of rotation. A tachogenerator is connected directly to the DC motor and produces voltage proportional to the angular velocity.
Tachogenerator DC motor

Inertia load Backlash Encoder Magnetic Gearbox with
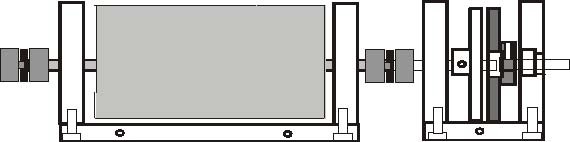
Fig. 1.1 The MSS setup
The servomechanism is connected to a computer where a control algorithm is realized based on measurements of angle and angular velocity. The system has no inner feedback for dead zone compensation. The accuracy of measurement of velocity is 5% while the accuracy of angle measurement is 0.1%. The armature voltage of the DC motor is controlled by PWM signal. For this reason the dimensionless control signal is the scaled input voltage, u(t) = v(t)/ v The admissible controls satisfy |u(t)| ≤ 1 and v = 12 [V].
max max
The measurement system is based on RTDAC4/PCI acquisition board equipped with a D/A and an A/D converters.
The I/O board communicates with the power interface unit. The whole logic necessary to activate and read the encoder signals and to generate the appropriate sequence of PWM pulses to control the DC motor is configured in the Xilinx® chip of the RT-DAC/PCI board. All functions of the board are accessed from the Modular Servo Toolbox which operates directly in the MATLAB®/Simulink® environment.
Features
- The set-up is fully integrated with MATLAB®/Simulink® and operates in real-time in MS Windows® 2000/XP.
- Real-time control algorithms can be rapidly prototyped. No C code programming is required.
- The software includes complete dynamic models.
- The User’s Manual contains a number of pre-programmed experiments familiarise the user with the system in a fast way.
1.2. Equipment and requirements
The following minimum configuration is required:
Hardware:
- Modular Servo System including the following modules: Input Potentiometer, DC Motor with Tachogenerator, Gearbox with output disk, Magnetic Brake, Inertia Load, Digital Encoder, Backlash module.
- Computer system based on INTEL or AMD processor.
- Specialised RT-DAC/PCI-D I/O board.
- Power Interface unit.
Software:
• MS Windows® 2000/XP, MATLAB® 7 (R14 SP2, SP3), R2006a, R2006b /Simulink® 6.x, Real Time Workshop and Real Time Windows Target toolboxes, MSS Control/Simulation Toolbox.
The Modular Servo Toolbox supports Matlab 7 (R14 SP2, SP3) and • MATLAB R2006a, R2006b.
Manuals:
- Installation Manual
- User’s Manual
![]() The experiments and corresponding to them measurements have been conducted by the use of the standard INTECO system. Every new system manufactured and developed by INTECO can be slightly different to those standard devices. It explains why a user can obtain results that are not
The experiments and corresponding to them measurements have been conducted by the use of the standard INTECO system. Every new system manufactured and developed by INTECO can be slightly different to those standard devices. It explains why a user can obtain results that are not
identical to these given in the manual.
1.3. Hardware installation
Hardware installation is described in the Installation Manual.
1.4. Software installation
Insert the installation CD and proceed step by step following displayed commands. Software installation is described in the Installation Manual.
2. Starting, testing and stopping procedures
2.1. Starting procedure
Invoke MATLAB by double clicking on the MATLAB icon. The MATLAB command window opens. Then simply type:
servo
MATLAB brings up the Servo Control Window (see Fig. 2.1). Pushbuttons indicate an action that executes callback routines when the user selects a menu item.
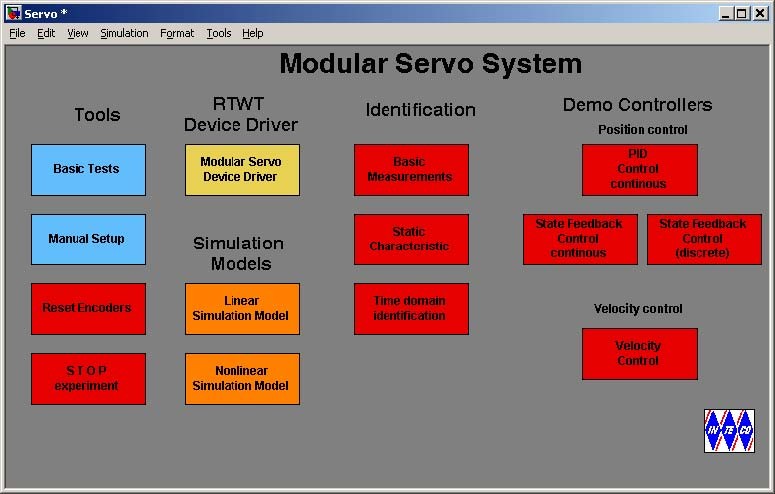
The Servo Control Window contains testing tools, drivers, models and demo applications. See section 3 for detailed description.
2.2. Testing and troubleshooting
This section explains how to perform the tests. These tests allow checking if mechanical assembling and wiring has been done correctly. The tests have to be performed obligatorily after assembling the system. They are also necessary if an incorrect operation of the system takes place. The tests are helpful to look for reasons of errors when the system fails. The tests have been designed to validate the existence and sequence of measurements and controls. They do not relate to accuracy of the signals.
First, you have to be aware that all signals are transferred in a proper way. Five testing steps are applied.
• Double click the Basic Tests button. The following window appears (Fig. 2.2):
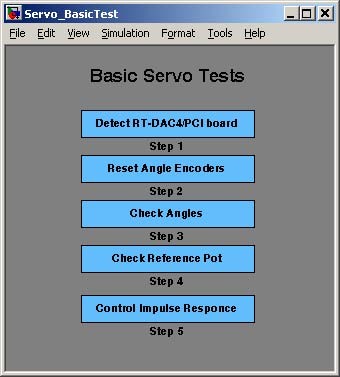
The first step in testing of the Modular Servo System is to check if the RT-DAC/PCI I/O board is installed properly.
• Double click the Detect RTDAC/PCI board button. One of the messages presented in Fig.
2.3 opens. If the board has been correctly installed, the base address, and number of logic version of the board are displayed.
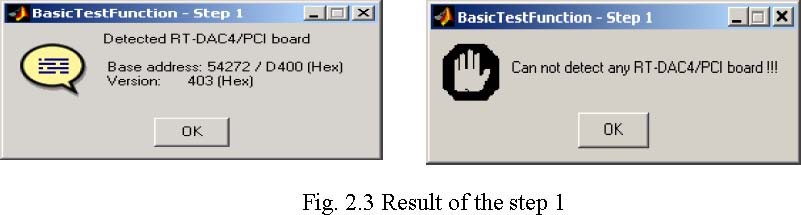
If the board is not detected check mounting of the board in a slot. The boards are tested very precisely before sending to a customer and only not correct assembly results errors.
In the next step one can to reset encoders. It set the beginning position of the servo system.
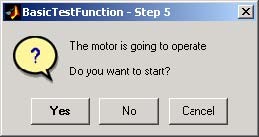
- Double click the Reset Angle Encoders button. When window (Fig. 2.4) will opens, click Yes option. The encoders will reset and zero position of the servo system will be stored as long as any errors of measurements will occur.
- Double click Check Angles button, next click Yes button and turn the inertia load by hand. The movement of the inertia is measured and displayed (Fig. 2.5 ).
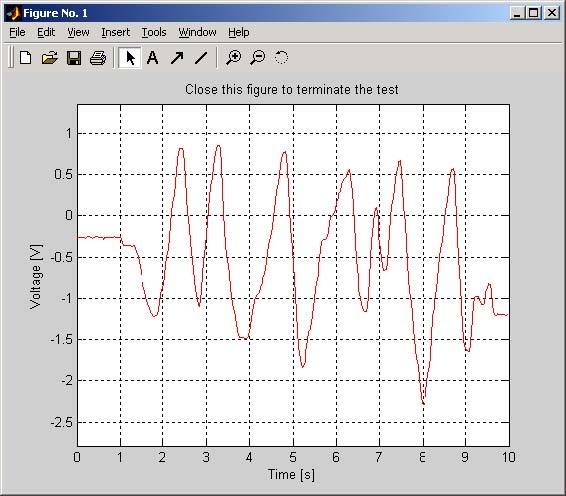
- To check if the potentiometer works correct double click the Check Reference Pot button. Next click Yes and turn the potentiometer right and left.
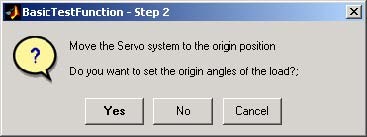
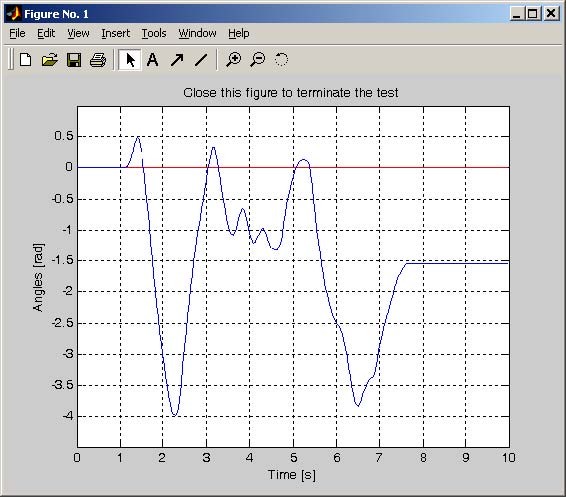
Fig. 2.6 shows an example of the proper measurements of the potentiometer position.
In the next step of the basic tests one can check if the control and measurements of angle and velocity in the MSS are correct. This experiment is not performed in real-time mode.
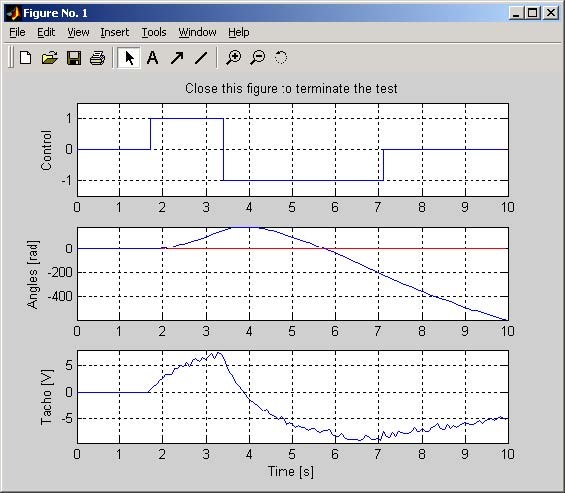
• Double click Control Impulse Response button and start experiment clicking Yes button.
The results of experiments are presented in Fig. 2.7. That control impulse has square wave form. The first part of the control signal is positive, and the second one is negative. Note that angle and velocity signals are positive at the beginning and next fall down to the negative values. It means that the measurements are correct. In the opposite case you have to reverse the plus and minus power cables of the DC motor.
3. Servo Control Window
The user has a quick access to all basic functions of the modular servo control system from the Servo Control Window. It includes tests, drivers, models and application examples.
Type at Matlab prompt servo command and Servo Control Window presented in Fig. 2.1 opens. Simultaneously start.m m-file is executed which set the default values of the coefficients of servo model Ks = 186 [rad/s] and Ts= 1.04 [s]. Also sampling time Tsis set
equal to 0.002 [s].
The window contains four groups of the menu items:
- Tools -Basic Test, Manual Setup, Reset Encoders and Stop Experiment,
- Drivers -RTWT Device Driver,
- Simulation Models: linear and nonlinear,
- Identification -Basic Measurements, Steady-State Characteristics and Time Domain Identification,
- Demo Controllers –PID Controller and State Feedback Controller applied to position control and PID controller applied to velocity control.
3.1. Basic test
The Basic Test tool was described in the previous section.
3.2. Manual setup
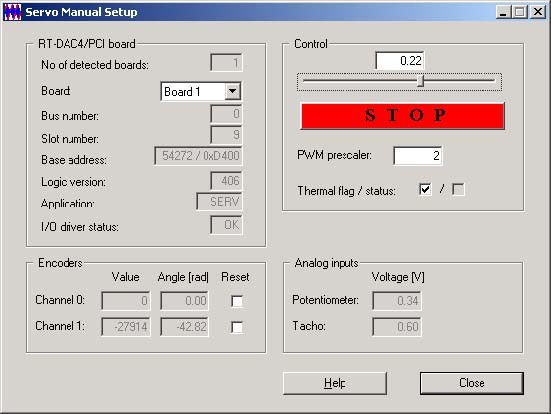
The Servo Manual Setup program gives access to the basic parameters of the laboratory modular servo setup. The most important data transferred from the RT-DAC4/PCI board and the measurements of the servo may be shown. Moreover, the control signals can be set. Double click the Manual Setup button and the screen presented in Fig. 3.1 opens.
The application contains four frames:
- RT-DAC4/PCI board,
- Encoders,
- Control and
- Analog inputs
All the data presented by the Servo Manual Setup program are updated 10 times per second.
• RT-DAC4/PCI board frame
The RT-DAC4/PCI board frame presents the main parameters of the RT-DAC4/PCI I/O board.
No of detected boards
Presents the number of detected RT-DAC4/PCI boards. If the number is equal to zero it means that the software has not detect any RT-DAC4/PCI board. When more then one board is detected the Board list must be used to select the board that communicates with the MSS control program.
Board
Contains the list applied to select the board currently used by the program. The list contains a single entry for each RT-DAC4/PCI board installed in the computer. A new selection executed at the list automatically changes values of the remaining parameters.
Bus number
Displays the number of the PCI bus where the current RT-DAC4/PCI board is plugged-in. The parameter may be useful to distinguish boards, when more then one board is used.
Slot number
The number of the PCI slot where the current RT-DAC4/PCI board is plugged-in. The parameter may be useful to distinguish boards, when more then one board is used.
Base address
The base address of the selected RT-DAC4/PCI board. The RT-DAC4/PCI board occupies 256 bytes of the I/O address space of the microprocessor. The base address is equal to the beginning of the occupied I/O range. The I/O space is assigned to the board by the computer operating system and may differ from one computer to another.
The base address is given in the decimal and hexadecimal forms.
Logic version
The number of the configuration logic of the on-board FPGA chip. A logic version corresponds to the configuration of the RT-DAC4/PCI boards defined by this logic.
Application
The name of the application the board is dedicated for. The name contains four characters. In the case of the modular servo system it has to be SERV string.
I/O driver status
The status of the driver that allows the access to the I/O address space of the microprocessor. The status displayed has to be OK string. In other case the driver HAS TO BE INSTALLED.
• Encoders frame
The state of the encoder channels is given in the Encoder frame.
Channel 0, Channel 1
The values of the encoder counters, the angles expressed in radians and the encoder reset flags are displayed in the Channel 0 and Channel 1 row. In this version MSS may use a single encoder module. In such a case only one channel presents the current data.
Value
The values of the encoder counters are given in the respective columns. The values are 24bit integer numbers. When an encoder remains in the reset state the corresponding value is equal to zero.
Angle [rad]
The angular positions of the encoders expressed in radians are given in the respective columns. When the encoder remains in the reset state the corresponding angle is equal to zero.
Reset
When the checkbox is selected the corresponding encoder remains in the reset state. The checkbox has to be unchecked to allow the encoder to count the position.
• Control frame
The Control frame allows to change the control signal.
Edit field, slider
The control edit box and the slider are applied to set a new control value. The control value may vary from –1.0 to 1.0.
STOP
The pushbutton is applied to switch off the control signal. When pressed the control value is set to zero.
PWM prescaler
The divider of the PWM reference signal. The frequency of the PWM control is equal to:
40
f = [KHz ]
pwm (1+ PWMprescaler )
Thermal flag / status
The thermal flag and the thermal status of the power amplifier. If the thermal status box is checked the power interface is overheated. If the thermal flag is set and the power interface is overheated the RT-DAC4/PCI board automatically switches off the PWM control signal.
• Analog inputs frame
The Analog inputs frame displays two measured analog signals.
Potentiometer
Presents the voltage at the output of the potentiometer blocks.
Tacho
Presents the voltage at the output of the tachogenerator.
3.3. RTWT Driver
The main driver is located in the RTWT Device Driver column. The driver is a software “go-between” for the real-time MATLAB environment and the RT-DAC/PCI I/O board. This driver serves the control and measurement signals. Click the Modular Servo Device Driver button and the driver window opens (Fig. 3.2).
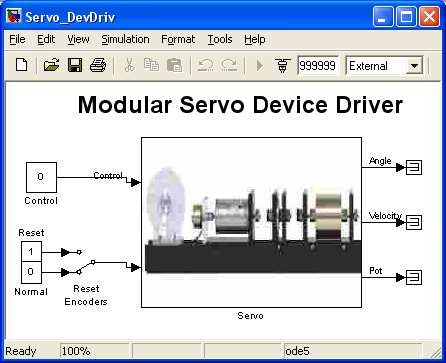
When one wants to build his own application have to copy this driver to a new model. The Reset Encoder input can be used in the real-time mode only.
Do not make any changes inside the original driver. They can be made only • inside its copy! Just in case make a copy from the installation CD.
The device driver has two inputs: control u(t) ⊂ [−1+1] and signal Reset. If signal Reset changes to one the encoders are reset and does not work. If signal Reset is equal to zero encoders normally work. It is important that Reset switch works only when real-time code is executed. It means that changing of state of the switch, when real time mode is not running, will not result. However when switching occurs when real time is running, encoders reset and starts measure when the switch returns to the zero (normal) position.
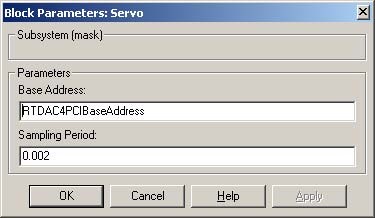
The mask of the servo block (presented at the right side) contains base address of the RT-DAC4/PCI board (automatically detected) and sampling period which default value is set to 0.002 sec. If one want to change during any experiment the default sampling time it must be done in this mask also.
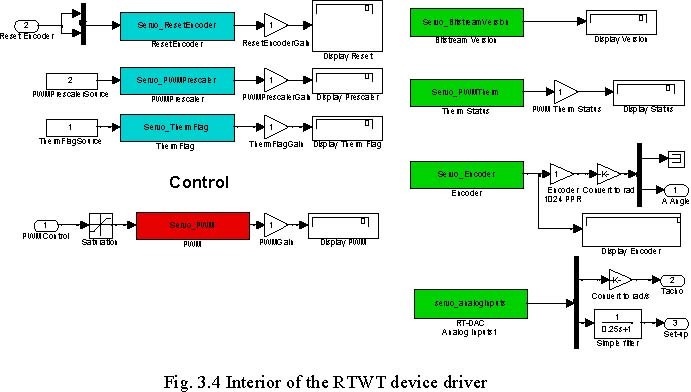
The details of the device driver are depicted in Fig. 3.4. The driver uses a functions which communicates directly with a logic applied at the RTDAC/PCI board. Notice, that the driver is ready to use a second (optional) encoder, as well.
Measurements Parameters
3.4. Simulation Models
There are two simulation models available for the servo system. The first one is a linear model and the second one is nonlinear. The linear model is used to design a controllers. The nonlinear model is used to check the quality of the designed control system.
Linear and Nolinear Simulation Model – the simulation models of the servo are located under these buttons. The external view of the simulation models is identical as the model described in the Modular Servo Device Driver except the Reset Encoder input and reference Potentiometer output which are not used in the simulation mode.
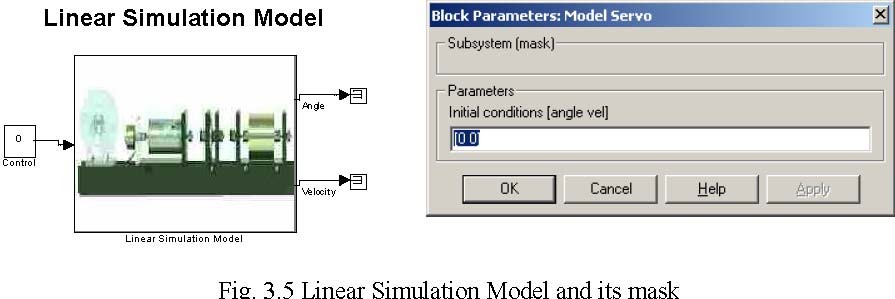
The vector of initial conditions of the state variables of the simulation models is the parameter available in the mask.
![]() The model has no constrained control (as real servo system). If you use the linear simulation model in a closed-loop system remember that control should
The model has no constrained control (as real servo system). If you use the linear simulation model in a closed-loop system remember that control should
satisfy u ≤1. You can include the Saturation block to limit control.
In the case of the nonlinear simulation model two additional parameters appear. The gain of the model and the vector which contains static characteristics of the servo system. Refer to section 4.

![]() Choose Fixed step solver options and set Fixed-step size equal to 0.002. It is necessary because the default value of the sampling time of the all real-time
Choose Fixed step solver options and set Fixed-step size equal to 0.002. It is necessary because the default value of the sampling time of the all real-time
models is equal to 0.002 [s].
3.5. Identification
The respective buttons in the group Identification of the Servo Control Window perform the following tasks:
Basic Measurements – contains a real-time Simulink model where a saw shape control signal is given as the input of the servo system and four velocities are plotted in a scope:
- measurements reconstructed from encoder,
- measurement directly from tachogenerator,
- filtered tachogenerator voltage using low pass Butterworth filter,
- filtered tachogenerator voltage using simple first order filter.
The experiment allows to decide which kind of velocity measurements can be used in following experiments.
Plot basic measurements push button -activates the plot_basic.m file to plot measurements visible in the scope in the previous experiment.
Static Characteristics -performs experiment aimed to measure of the static characteristics of the loaded DC motor (angular velocity [rad/s] vs. input voltage [dimensionless] in the steady state). The characteristics can be measured for the servo system with or without magnetic brake module. The measurements are stored in the ChStat.mat file.
Plot & Save Characteristics -uses plot_stat.m file which plots measured characteristics, performs some normalisations of the data, and saves characteristics in servo_chstat.mat file.
Time Domain Identification – opens the real-time Simulink model which starts identification based on a step system response.
The button Identify Model -takes advantage of identification data and calculates coefficients of a linear model of the servo system. The surface method is applied by the identification procedure.
3.6. Demo Controllers
The respective buttons in the column Demo Controllers perform the following tasks:
Position control
PID Control Continous -contains the Simulink model for real-time experiments in closed-loop with PID position controller, and simulation model of the PID controlled servo system.
State Feedback Control -opens the Simulink model to start real-time experiments for closed-loop system with state feedback. This model can be used for experiments with LQ or deadbeat controllers. Also simulation model of the closed-loop system is included under this button.
All the Simulink models mentioned above are examples of position control problems.
Calculate LQ controller – uses Servo_calc_lq.m file to obtain state feedback controller coefficients by solving the appropriate LQ problem. In the Servo_calc_lq.m file one can set matrices of the objective function to obtain appropriate behaviour of the system.
Velocity control
PID Controller -opens the Simulink model to start-real time experiments for closed-loop system with velocity PID controller.
4. Mathematical model of the servo system
4.1. Linear Model
A DC motor with negligible armature inductance (Fig. 4.1)
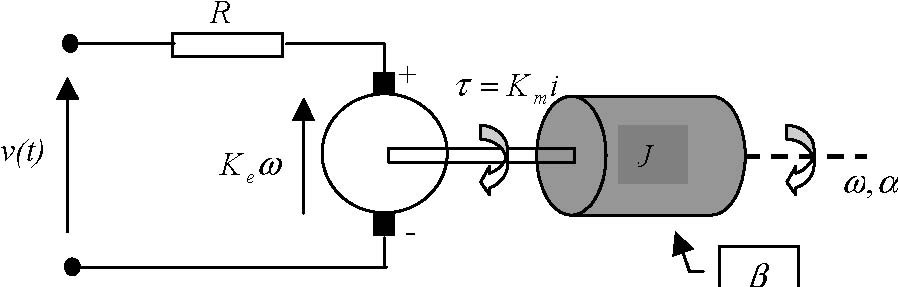
Fig. 4.1 Diagram of DC motor
is described by two classical equations: electrical v(t) = Ri(t) + Keω(t)
and mechanical Jω& (t) = Kmi(t) − βω(t)
where: v(t) is the input voltage, i(t) is the armature current,
ω(t) is the angular velocity of the rotor, R is the resistance of armature winding, J is the moment of inertia of the moving parts, β is the damping coefficient due to viscous friction, Keω(t) is the back EMF,
and τ= Kmi(t) is the electromechanical torque.
This model is linear because static and dry kinetic friction, as well as saturation are neglected. By combining the electrical and mechanical equations we obtain the equation of a first order inertial system
Ts ω& (t) = −ω(t) + K sm v(t)
where the motor time constant Tsand motor gain K sm are given by
RJ Km
Ts = , Ksm = .
β R + KK β R + KK
em em
The transfer function has form
ω(s) Ksm
G(s) ==
v(s) Tss +1 The transfer function for the motor position has form: α (s) Ksm
G(s) ==
v(s) s(Tss +1)
Because of the control applied in the system, is a PWM signal we assume the dimensionless control signal as the scaled input voltage, u(t) = v(t)/ vmax . The admissible controls satisfy |u(t)| ≤ 1. Respecting also K = Kv we obtain transfer functions in the forms:
s sm max
| Velocity transfer function | Angle transfer function |
| 1( ) ( )( ) + == T s K u s sG s s sω | 1)(( ) ( )( ) + == s T s K u s sG s s sα |
The model can be written using a state space notation. Let x = col(x1, x2 ) be the state vector where x1 is the angle α (in [rad]) determining the position of the motor shaft, and x2 =ω is the respective angular velocity (in [rad/s]). Time t is measured in [s].
The state equations read
x& = x
12 x& 2 = ax 2 + bu
where 1 Ks
a =− < 0, b => 0. Ts Ts
The equivalent classical matrix state space notation has the form
| Bu Ax x +=& Cx y = | where: ⎢⎣○=A 0 0 | ⎥⎦− sT 1 1, | ⎥⎦ ⎢⎣○ = s s T KB 0 , | IC = . |
|---|
The system can be classified as a multivariable (SIMO) because it has two measurable state variables and one control variable. The parameters Tsand Ks must be identified by a user.
The default values which can be used before identification experiments are as follows: = 12 [V], T = 1.04 [s], K = 186 [rad/s], which gives a =−0.961[s−2], and
max ss 2
b = 178.8 [rad/s ].
These values were obtained by the manufacturer for the DC motor with tachogenerator loaded by the inertia module and connected with the gearbox module equipped with output disk.
4.2. Nonlinear model
In most cases small signal changes are presupposed for the design of control algorithms, so that the control system might be considered linear. In some applications however, nonlinearities in the control loop have to be taken into account. This includes non-linear static characteristics such as hysteresis and saturation, which may occur if the following devices are applied: operational amplifiers, actuators, finite word length in A/D and D/A converters. Often the signal constraint first appears for the control variable. We will assume a nonlinear model of the DC motor in the form
x& = x
12
x& 2 = c(u − g(x2 ))
where the state variables x1, x2 and control u are defined as in the linear model.
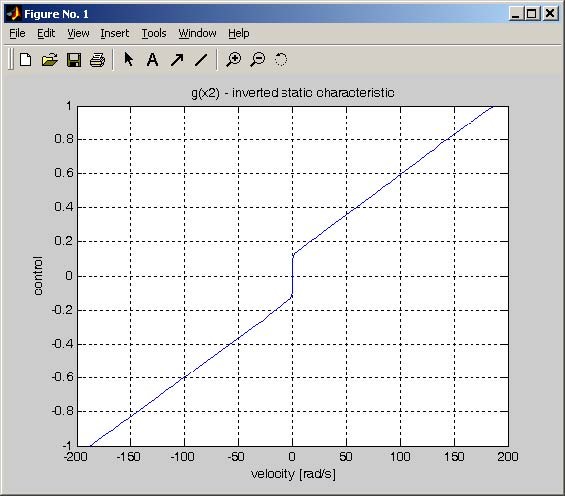
The function g is the inverted steady state characteristics of the system, which can be determined experimentally (see section 6.2). The original steady state characteristics (see Fig. 6.8) is obtained from measurements. The results of measurements undergo a preliminary treatment consisting of scaling (to express them in appropriate units) and a shift (to remove the bias). The function g is presented in Fig. 4.2. An interesting property of the gfunction is that it is discontinuous at zero and shows distinct effects of dry friction in a vicinity of the origin.
![]() The static characteristics was obtained for the system consists of DC motor, inertia load, encoder and gearbox modules. If a magnetic break module is
The static characteristics was obtained for the system consists of DC motor, inertia load, encoder and gearbox modules. If a magnetic break module is
added to the system a measured characteristics are quite different.
The c coefficient was identified and c = 206 [rad/s].
5. RTWT model
In this section the process of building your own control system is described. The Real Time Windows Target (RTWT) toolbox is used. An example how to use the MSS software is shown later in section 6. In this section we give indications how to proceed in the RTWT environment.
Before start, test your MATLAB configuration and compiler installation by building and running an example of real-time application. Real-time Windows Target Toolbox includes the model rtvdp.mdl. Running this model will test the installation by running Real-Time Workshop, Real-Time Windows Target, and • the Real-Time Windows Target kernel. In the MATLAB Command Window, type rtvdp Next, build and run the real-time model.
To build the control application that operates in the real-time mode the user has to:
- create a Simulink model of the control system which consists of the Modular Servo Device Driver and other blocks selected from the Simulink library,
- build the executable file under RTWT,
- start the real-time code to run from the Simulation/Start real-time code pull-down menus.
5.1. Creating a model
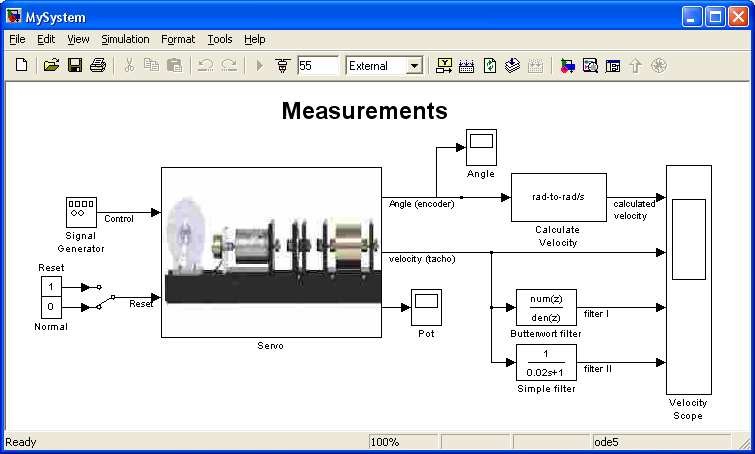
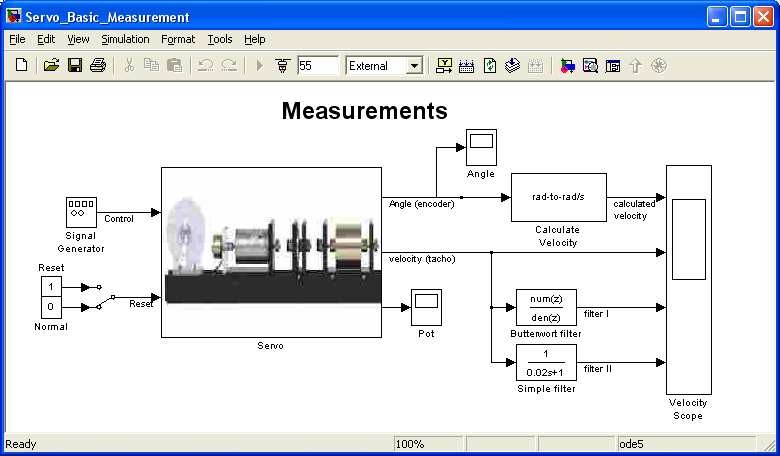
The simplest way to create a Simulink model of the control system is to use one of the models available from the Servo Control Window as a template. For example, click on the Basic Measurements button and save it as MySystem.mdl name. The MySystem Simulink model is shown in Fig. 5.1.
Now, you can modify the model. You have absolute freedom to modify the model and to develop your own control system. Remember to leave the Servo driver block in the window. This is necessary to work in RTWT environment.
Though it is not obligatory, we recommend you to leave the scope. You need a scope to watch how the system runs. The saturation blocks are built in the Servo driver block. They limit currents to DC motor for safety reasons. However they are not visible for the user who may amaze at the saturation of controls. Other blocks remaining in the window are not necessary for our new project.
Creating your own model on the basis of an old example ensures that all-internal options of the model are set properly. These options are required to proceed with compiling and linking in a proper way. To put the Servo Device Driver into the real-time code a special make-file is required. This file is included to the MSS software.
You can apply most of the blocks from the Simulink library. However, some of them cannot be used (see RTW or RTWT references manual).
The scope block properties are important for appropriate data acquisition and supervising how the system runs.
The Scope block properties are defined in the Scope property window (see Fig. 5.2). This window opens after the selection of the Scope/Properties tab. You can gather measurement data to the Matlab Workspacemarking the Save data to workspace checkbox. The data is placed under Variable name. The variable format can be set as structure or matrix. The default Sampling Decimation parameter value is set to 1. This means that each measured point is plotted and saved. Often we choose the Decimation parameter value equal to 5. This is a good choice to get enough points to describe the signal behaviour and to save the computer memory. In this case the time space of the plot is equal to 0.01 [s].

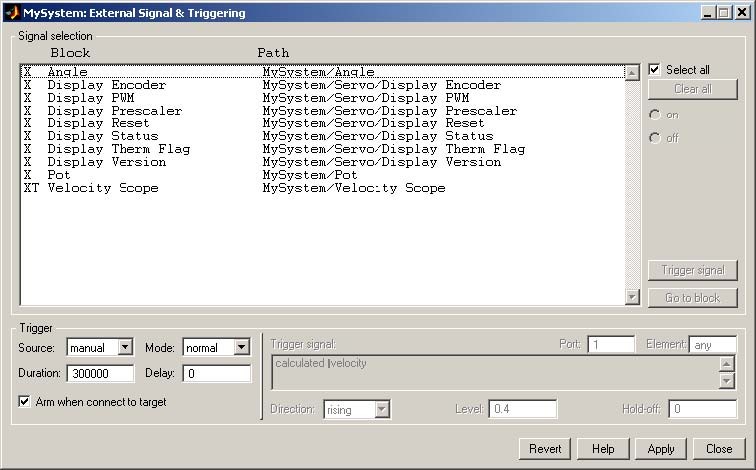
When the Simulink model is ready, click the Tools/External Mode Control Panel option and next click the Signal Triggering button. The window presented in Fig. 5.3 opens. Select Select All check button, setSource as manual, set Duration equal to the number of samples you intend to collect and close the window.
5.2. Code generation and the build process
Once a model of the system has been designed the code for real-time mode can be generated, compiled, linked and downloaded into the computer.
The code is generated by the use of Target Language Compiler (TLC) (see description of the Simulink Target Language). The make-file is used to build and download object files to the target hardware automatically.
First, you have to specify the simulation parameters of your Simulink model in the Simulation parameters dialog box. The RTW page appears when you select the RTW tab (Fig. 5.4). The RTW page allows you to set the real-time build options and then to start the building process of the RTW.DLL executable file.
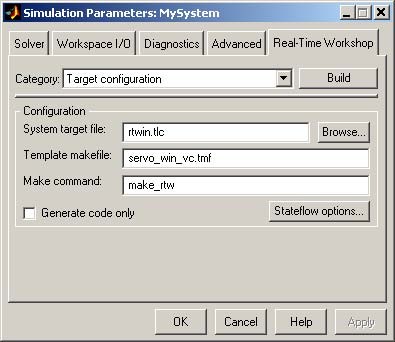
The system target file name is rtwin.tlc. It manages the code generation process. The servo_win_vc.tmf template make-file is devoted to C code generation using the Microsoft Visual C++ compiler.
If the Matlab 7.0.4 version is used a third party compiler is not requested. The built-in Open Watcom compiler is used to creating real-time executable code for RTWT.
The Configuration parameters page for MATLAB 7.04 is shown in Fig. 5.5. Notice that rtwin.tmf template makefile is used. This file is default one for RTWT building process.
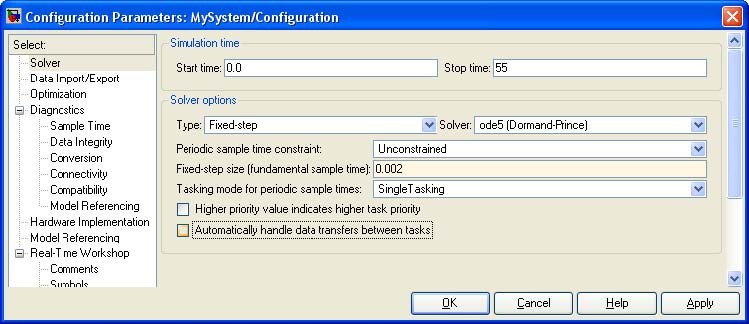
The Solver page appears when you select the Solver tab (Fig. 5.6). The Solver page allows you to set the simulation parameters. Several parameters and options are available in the window. The Fixed-step sizeeditable text box is set to 0.002 (this is the sampling period in seconds).
The Fixed-step solver is obligatory for real-time applications. If you use an arbitrary block from the discrete Simulink library or a block from the driver
• library remember that different sampling periods must have a common divider.
The Start time has to be set to 0. The solver has to be selected. In our example the fifth-order integration method − ode5 is chosen.
If all parameters are set properly you can start the DLL executable building process. For this purpose press the Build push button on the RTW page (Fig. 5.4).
Successful compilation and linking processes generate the following message:
### Created Real-Time Windows Target module MySystem.rwd.
### Successful completion of Real-Time Workshop build procedure for model: MySystem
Otherwise, an error massage is displayed in the MATLAB command window.
6. Basic Assignments
All experiments described in this manual are performed with servo system consisting of the following modules: DC motor with tachogenerator, inertia load, encoder and gearbox with output disk. In one experiment additionally the backlash module is applied.
6.1. Basic measurements
In this section quality of measurements in the servo system is concerned. The shaft angle is measured with high accuracy by an incremental encoder. The shaft angular velocity if is not used the tachogenerator must be observed i.e. reconstructed from the angle measurements. If the tachogenerator is used as a velocity sensor then its voltage comes together with disturbances, therefore it must be filtered.
The Signal generator block produces a saw shape control signal for the servo system. This shape was selected to demonstrate the full range of the control values.
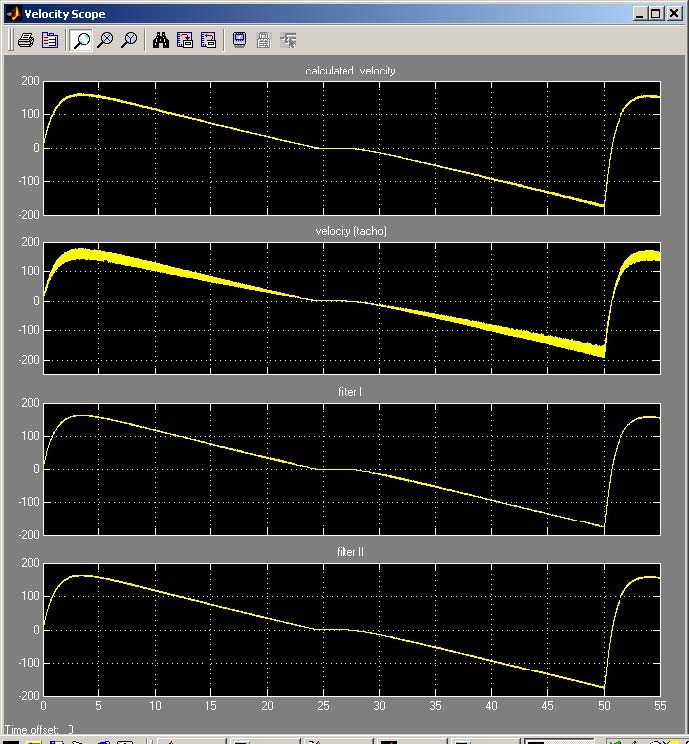
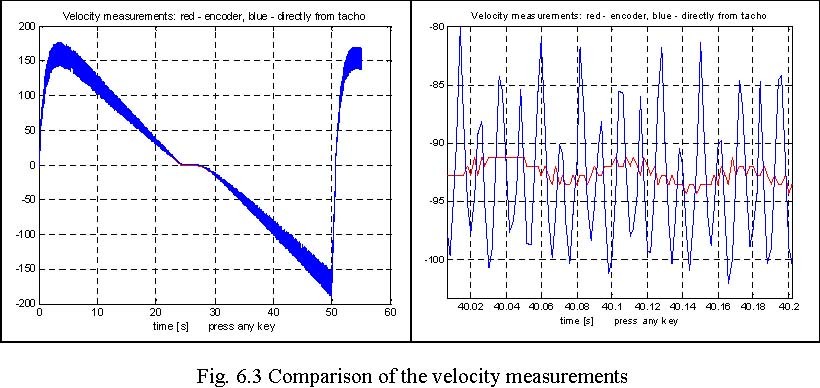
The all velocity measurements are given in Fig. 6.2. One can see that the worth result are obtained for output voltage of the tachogenerator. The reconstructed velocity (from encoder measurements of the angle) is the best one. Also if the appropriate filter is applied the measurements are satisfactory. Two types of the filter are applied: the fourth order Buterworth filter and a simple first order filter. Details and differences between the measurements are shown in Fig. 6.3 and Fig. 6.4. A user can choose which a velocity measurement will use in the own real-time experiments.
Modular Servo System -User’s Manual
| 150 200 | Filtered velocity: red -Butterworth filter, blue -simple filter | -91 -90.5 | Filtered velocity: red -Butterworth filter, blue -simple filter | |
| 100 |
|
-91.5 |
|
|
| 0 -200 -150 -100 -50 050 | 10 20 30 40 50 60 time [s] press any key | -94.5 -94 -93.5 -93 -92.5 -92 | 40 | 40.02 40.04 40.06 40.08 40.1 40.12 40.14 40.16 40.18 40.2 time [s] press any key |
6.2. Steady state characteristics of the DC servo
Double click the Static characteristics button in Servo Control Window. The window given in Fig. 6.5 opens. In this window one defines the minimal and maximal control values and a number of measured points. Also the control order can be set as: Ascending, Descending or Reverse.
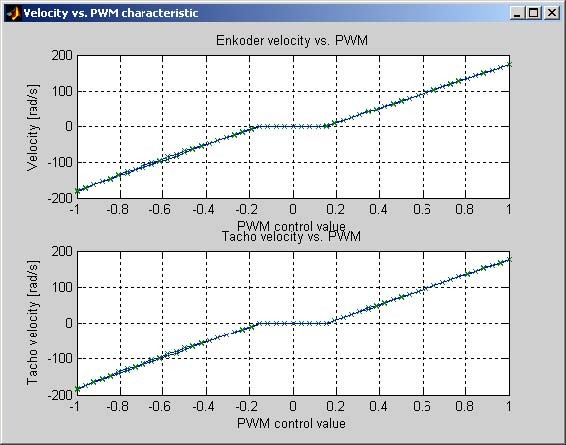
The Run button starts experiment. The constant value of control activates the DC motor so long as is required to obtain a steady state of the shaft angular velocity. Then, the velocity is measured and the control value is changed to the next constant value and DC motor is activated again. These steps are repeated to the end of the control range. Simultaneously the all measurements are displayed in the screen (see Fig. 6.6). There are two sources of DC motor velocity. the reconstruction from the incremental encoder pulses and the tachogenerator voltage. After identification process the measurements are saved in the ChStat.mat file.
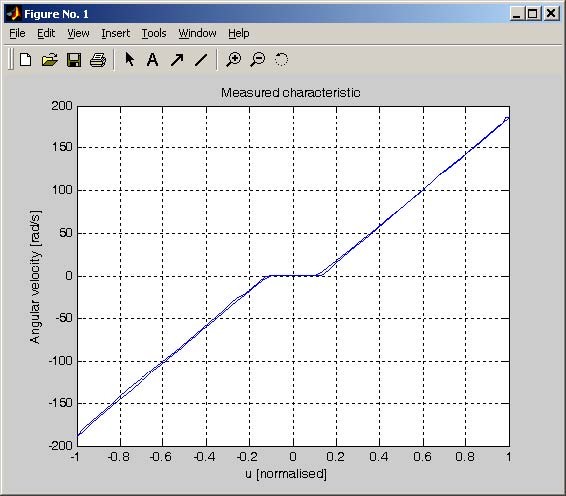
When the measurements are finished, close the window and double click the Plot & save button. The ChStat.mat file is loaded and static characteristics is plotted (see Fig. 6.7). Notice that when the characteristics is measured in Reverse mode ( the control has been changed from –1 to +1 and reverse), there are two plots slightly different. Next, the characteristics is averaged and shifted to zero in points where the static friction is too large for the control value. Next the plot (see Fig. 6.6) is drawn and the characteristics is saved in the servo_chstat.mat file. If this file exists it is rewritten.
Angular velocity [rad/s]
200
150
100
50
0
-50 -100 -150 -200
Static characteristic of DC servo

u [normalised]
Collecting data for the static characteristics is not repeated frequently. Please do not forget to save the old characteristics (with an appropriate description) in a safe place. The details are included in the plot_stat.m file which executes all mentioned above operations.
The characteristics saved in the servo_stat.mat file is used in the construction of a nonlinear model of the servo system.
6.3. Time domain identification
An identification task is to find the parameters Tsand Ks of the linear model of the servo system described by the transfer function
xs K
2( ) s
G(s)= = (6.1)
u(s) Ts s+ 1 in such a way, that the states of the model fit the experimental data. The step input signal u(t)= 1(t) is applied to the servo system and the velocity vs. time is acquired. Next, the surface method is applied to find the system parameters.
6.3.1. Identification task by the surface method
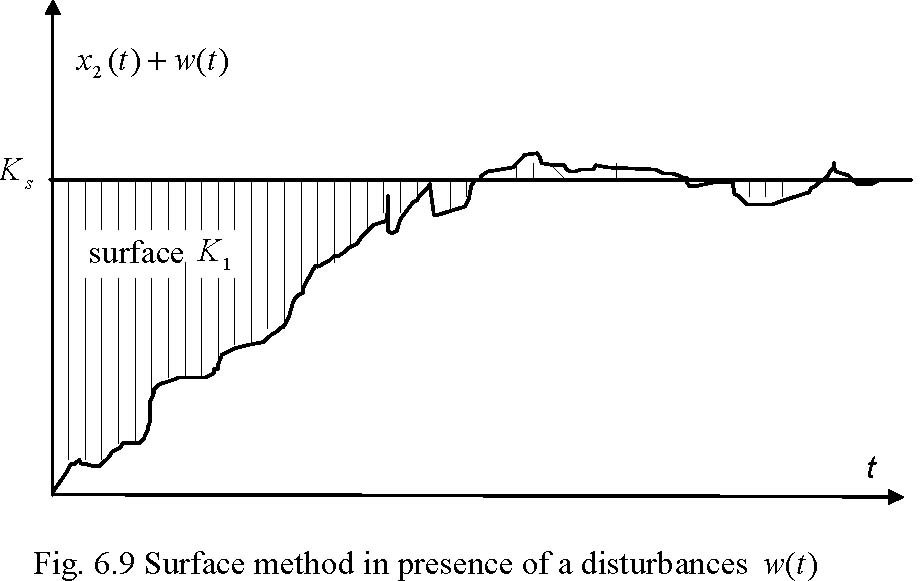
A velocity is denoted as x2(t). Applying the model (6.1) the required parameters KS and TS can be calculated using the following relations:
Ks = lim x2(t), t →∞
Ts = KK1 s where K1 = lim ∫ 0t (Ks − x2(λ))dλ,t →∞
The surface method is useful identification algorithm in the presence of disturbances. In this case the integral formula filtrates the measurement noises. Fig. 6.9 shows a typical application of this method to a DC servo identification problem.
6.3.2. Time domain identification experiment
In this experiment MSS includes the following modules: the DC motor with tachogenerator, inertia load, encoder module and gearbox module with the output disk. The magnetic break module can be added but in such a case the identified parameters of the system will be different.
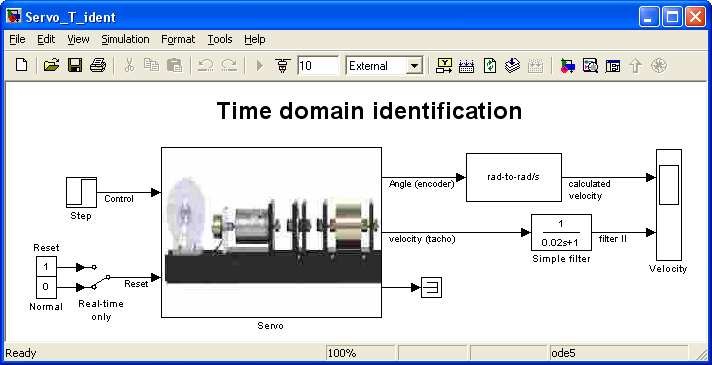
To start the identification experiment type servo at the MATLAB prompt and Servo Control Window appears. Now, double click the Time domain identification button. The model shown in Fig. 6.10 opens.
Build model (in the case if it has not been done before). Next, select the Simulation/connect to target option and click the Simulation/Start real-time code. The servo starts to move and one can observe the velocities displayed in the screen (see Fig. 6.11).
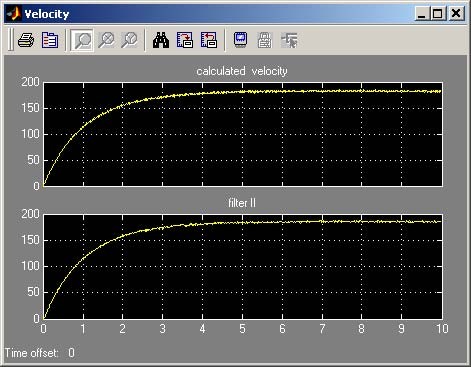
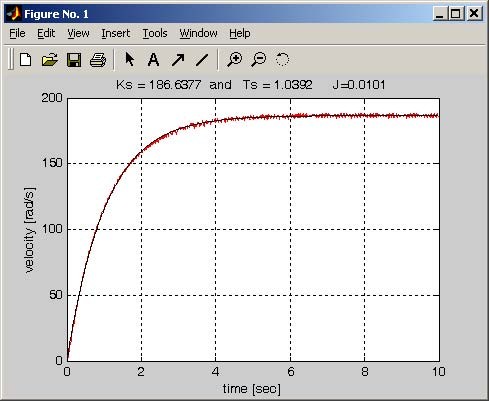
Click the Calculate model button. This action starts the plot_ident.m file where the surface method is applied and parameters of the servo model are calculated. Next, Fig. 6.12 opens and two plots are displayed in the screen
- velocity obtained from the measurements (red),
- velocity calculated from the model (black).
On the top of the figure the calculated coefficients and mse corresponding to data fitting are displayed. The coefficients are also displayed in the Matlab command window.
7. Advanced Assignments
7.1. PID position control
A PID controller is the most common form of feedback. In process control today, more than 95% of the control loops are of PID type, most loops are actually PI control. PID controllers are today present in all areas where control is used.
In this section a problem of position control of the servo is concerned. The background to simple tuning methods is introduced.
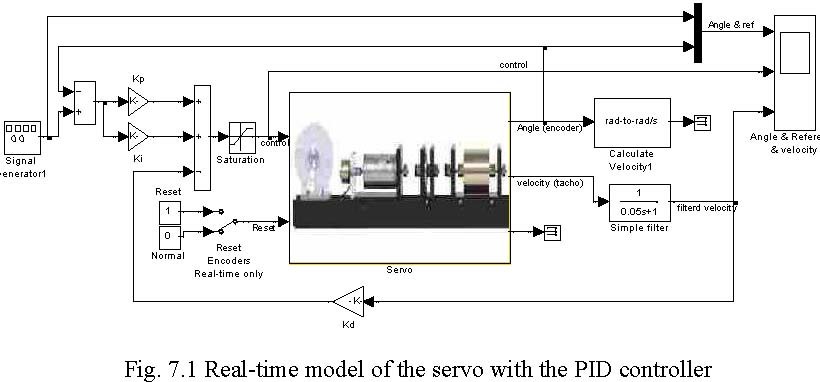
All real-time experiments related to the PID position control are performed using the model given in Fig. 7.1.
PID controller
Angle & Reference & velocity
Ki Generator1
Kd
The transfer function of a continuous PID controller used in this manual has the form:
u(s) KI
K(s)= =K p ++ sK D
ε (s) s
where: ε -error , K -gain coefficient, K -integral coefficient and K -derivation coefficient.
pI D
P controller
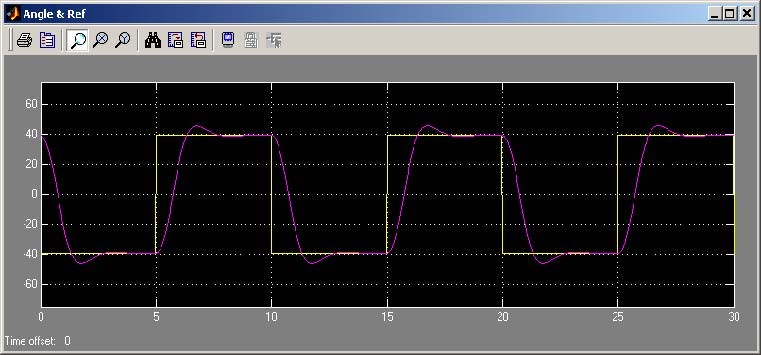
A goal of the control is to track a reference signal which is defined as a square wave. In this section P controller is investigated.
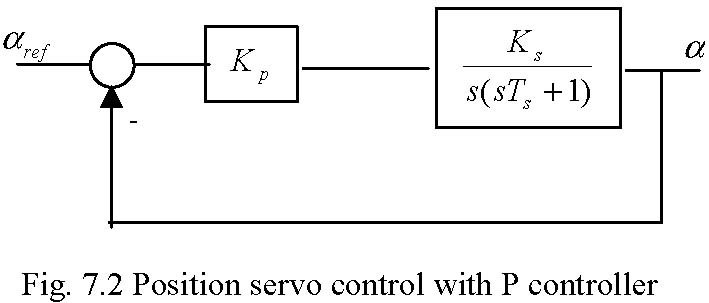
The diagram of the closed loop system is shown in Fig. 7.2. It is known that increasing gain in the considered system leads to oscillation. To test the real-time system for different gains of the P controller click PID control continuous button in Servo Control Window. The model given in Fig. 7.1 opens. We start with small value of the gain of the P controller. Type K=[0.0064 0 0] at the MATLAB prompt. It set proportional coefficient Kpof the P controller. Assuming a desired
range of change of the output disk equal to pi/8 set reference input signal equal to 100*pi/8 (it is the measured angle at the input to the gearbox). Also set frequency of the reference input to
0.05 Hz and sample time to 0.002.
• Build the model.
• Click the Simulation/connect to target and Start real-time code options to start
experiment. Next repeat the experiment for setting Kp = 0.0127 and Kp = 0.0254 .
The results of all experiments are given in Fig. 7.3 and Fig. 7.4. Note that oscillations of the system response appear if Kp = 0.0127 and Kp = 0.0254 .
Position control with P controller
80
60
40
20
0 -20 -40 -60 -80 0 5 10 15 20 25 30
| Kp=0.025 | 4 | |||||
| Kp=0.0064 | ||||||
| Kp=0.0127 | ||||||
time [s]
Note, that the real system is nonlinear therefore the oscillations are damped very quickly. The controls shown in Fig. 7.4 do not reach zero. It is due to the dead zone of the system which can be observed at steady state characteristics given in Fig. 6.8 and is equal about +/
0.15. The non active controls belong to this range. Note, that the control saturates for Kp = 0.0254 .
Controls
1
0.8
0.6
0.4
0.2
0 -0.2 -0.4 -0.6 -0.8
-1
| Kp= | 0.0064 | ||||
| Kp=0.01 | 27 | ||||
| Kp | =0.0254 | ||||
0 5 10 15 20 25 30 time [s]
In the table below steady state error is shown for the gain coefficients applied in these experiments. In accordance with theory if the Kp increases the steady state error decreases.
| K | 0.0064 | 0.0127 | 0.0254 |
|---|---|---|---|
| ∞ε | 20 % | 9.1 % | 4.8 % |
PD controller
The main goal of the controller tuning is to obtain the standard second order system step response. The general form of the second order transfer function is
ω 2
G (s) = n ss2 + 2ζω ns +ωn 2
If 0 <ζ < 1, then the step response of Gs (s) exhibits an exponentially damped sinusoidal character with the following features:
−ζπ ![]() 1−ζ
1−ζ
- percentage overshoot p% = 100 e 2
- 2% settling time ts = 4 ζω n
π
• time to peak tp = ![]() ωn 1−ζ 2
ωn 1−ζ 2
For given p% and ts one can calculate the damping coefficient ζ and natural frequency ωn . Comparing a transfer function of the closed-loop system, which contains coefficients of controller, with the standard transfer function Gs (s) one can calculate the controller coefficients.
EXAMPLE
Assume that we want to design PD controller for the position control of the servo system as it is shown in Fig. 7.5: Note that at the first glance the state feedback controller is used. But
dα
remember that ω= . For this reason the applied controller is PD type.
dt
The requirements corresponding to the dynamics of the closed-loop system are as follows:
- settling time ts ≤ 2.5[s]
- and maximal overshoot p% ≤ 10
controller
servo
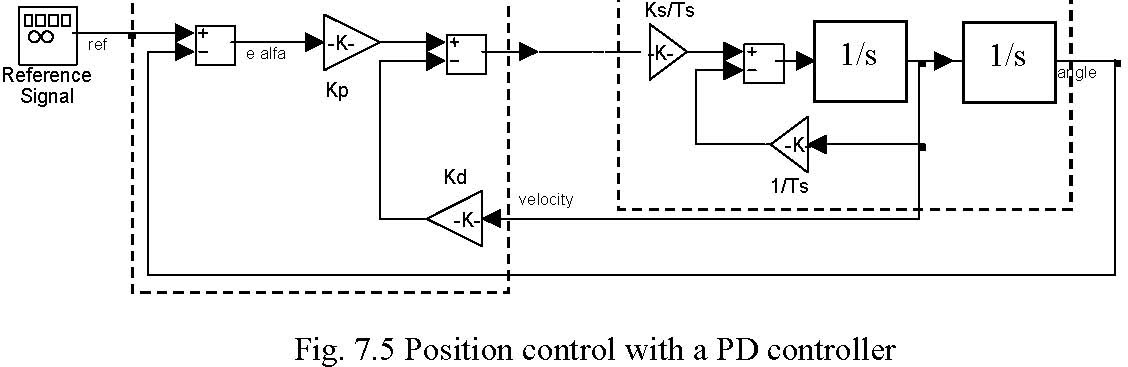
K
The servo system has the transfer function G(s) = s . The transfer function of the
s(Tss +1) PD controller is K(s) = Kp + KD s . The default values of the system coefficients are Ks = 186 [rad/s] and Ts= 1.04 [s].
Closing the control system we obtain the transfer function in the form
K pKs
Ts
G (s) = . z 2 KsKD +1 K pKs
s + s + Ts Ts
Substituting values for the coefficients into the transfer function we obtain
178.846 Kp
Gz (s) = . s2 + s(178.846 KD + 0.9615) +178.846 Kp
The following relationships are obtained by comparing the transfer function with the standard transfer function of the second order system
178.846 Kp =ωn 2,
2ζω n = 178.846 KD + 0.9615 .
Considering the formula and the condition for settling time ts ≤ 2.5[s] one obtains the
inequality KD ≥ 0.0125 . Consequently, respecting the formula and condition p% ≤ 10 related to the assumed
percentage overshoot one can calculate an unknown value as ζ= 0.5912 , later ωn = 2.7039
and Kp = 0.0409 .
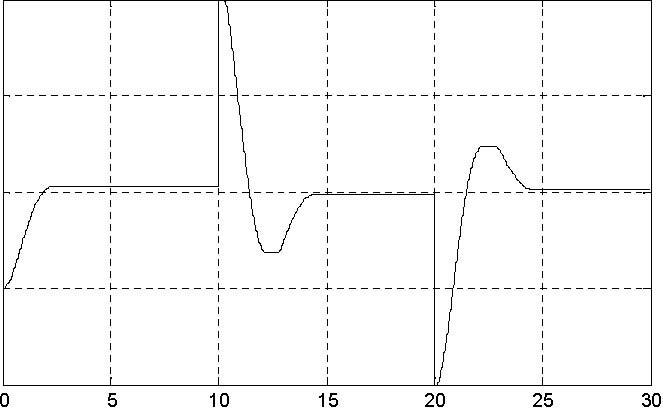
To check if the behaviour of the closed-loop system is consistent with requirements one can use the simulation method. Type at the Matlab prompt K=[0.0409 0 0.0125] to save the coefficients of the PD controller in the workspace. Click the PID controller & linear model button. The model depicted in Fig. 7.6 opens. Note, that the linear model of the servo is applied. The simulation results are shown in Fig. 7.7.
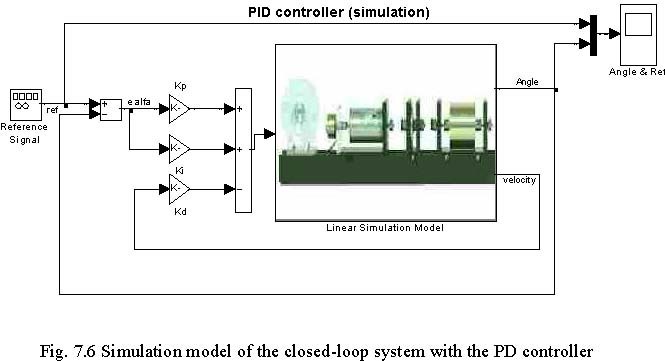
The percentage overshoot is too large, namely 16.4%. However the settling time is equal to 2.4[s] what is a satisfactory result. The steady state error is equal to 1.2% what shows that the goal of the control is satisfied but the requirement related to the percentage overshoot is missed.
Before redesigning a controller a real time experiment should be performed. Click the PID control continuous button. Click PID controller and model presented in Fig. 7.1 opens. Build it and start the real-time code. The results are presented in Fig. 7.8. Notice, that the response of the real system always differs slightly from the simulated one.

To see in details differences between the real time and simulation responses of the closed-loop system execute the servo_plot_pid.m file. This file is included in the Servo Toolbox but is accessible only from Matlab Command Window. The plot is depicted in Fig. 7.9. The table below includes the details read from the figure.
| Simulation | Real-time experiment | |
| st [s] | 2.4 | 3 |
| p% [%] | 16.5 | 8.14 |
| Steady state error [%] | 0.2 | 4.02 |
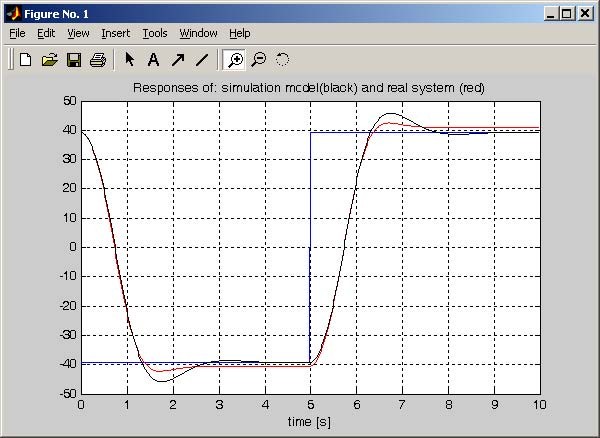
The overshoot of the real-time experiment is small but the steady state error is too large and the settling time is too long.
We are trying to increase proportional coefficient Kp of the PD controller. It will increase the overshoot (that is an admissible step) and decrease the steady state error (to a value which is required) and shorten the settling time what is required too.
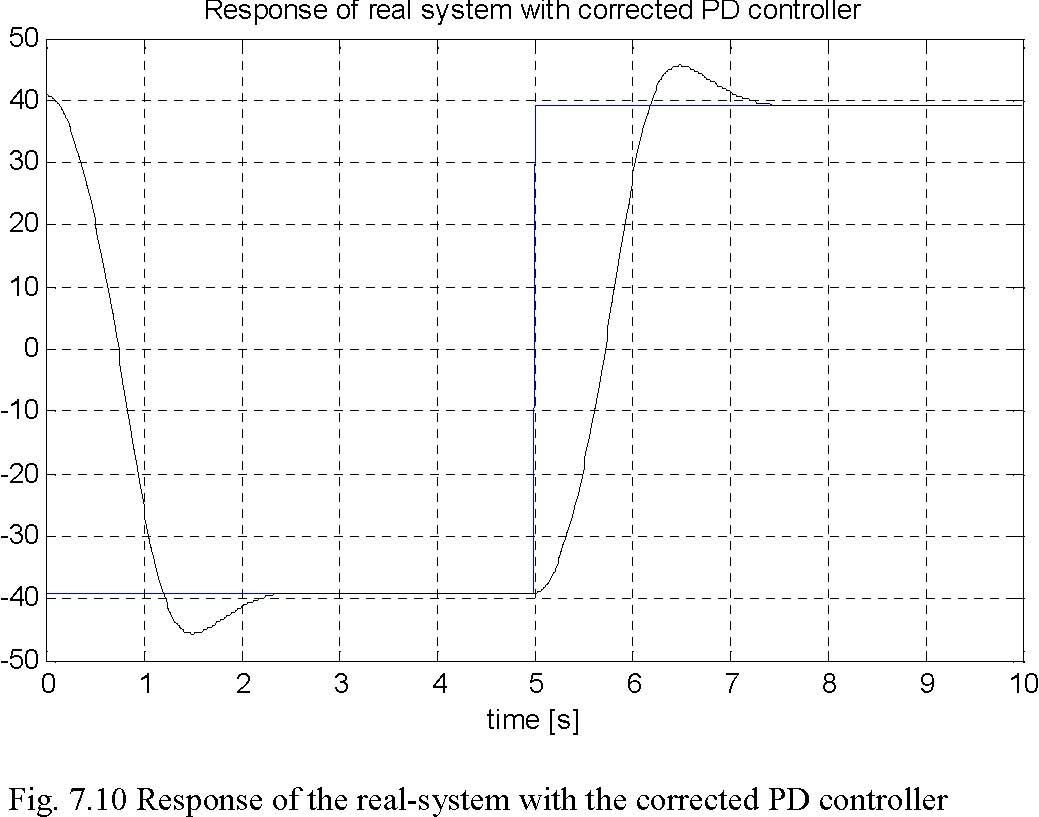
Type at Matlab prompt: K=[0.0609 0 0.0125] and repeat the real-time experiment with the PD controller and observe the results in the scope of the model. To see all details of responses vs. time type the following commands:
a=1;b1=length(PD_C.time); t=PD_C.time(a:b); a=1; b=10/(t(2)-t(1)); %plot only first 10 seconds of response t=t(a:b);plot(t,PD_C.signals(1).values(a:b,1), b ,t,PD_C.signals(1).va lues(a:b,2), k );grid;
title( Responses of: real system with corrected PD controller ); xlabel( time [s] );
The plot which has been obtained is shown in Fig. 7.10 The values of the percentage overshoot, settling time and steady state error are as follows:
p = 15.7 [%] , t = 2.23 [s] and ε= 0.33 [%].
% s ∞
The overshoot is greater than the assumed one but the settling time is fine and the steady-state error is perfect. We can conclude that the goal of the control is fully satisfied and that the PD controller just designed works well.
time [s]
PID controller
Now we try to apply the PID controller. The assumptions of design are defined as in the previous experiments. As far as operation and effectiveness are concerned the PID control is compared to PD control.
In the first step we define integrating (I) part of the PID controller. Type at Matlab prompt: K=[0.0609 0.1 0.0125] . Notice, that integral coefficient Ki = 0.1. The integral part helps to reduce the steady-state error. Click the PID control continuous button. Click PID controller and the model shown in Fig. 7.1 opens. Build it and start the real-time code. The results are given in Fig. 7.11. The dashed line corresponds to this experiment. One can see that the overshoot is too large. It is equal to 43%. The settling time increases with relation to PD controller up to 3.1 [s] and steady-state error decreases to 0.11 %. Now, set derivative coefficient as K = 0.0325 what should limit the overshoot. Also take K = 0.1. It should
Dp
also shorten the settling time. Type at the Matlab prompt K=[0.1 0.1 0.1325] and repeat the experiment.
The results are drawn in Fig. 7.11 with solid line. Now the parameters of the time response of the system are as follows: the settling time ts = 1.8 [s]. This is significantly shorter than
before. The percentage overshoot is p = 14.5 %. This is a slightly better result than that
%
obtained with PD controller. The steady state error is ε∞ = 0.12 %.
Position control with PID controller
60
40
20
0
-20
-40
-60 012 34 567 8910
| K= | [0.0609 0.1 0.0125] | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| K=[0. | 1 0.1 0.032 | 5 | |||||||
time [s]
Position control with backlash module
In this section position control problem is considered when the backlash exists in the servo system as is shown in Fig. 7.12.
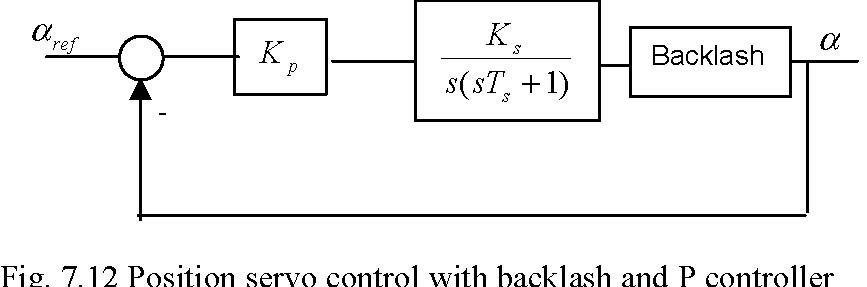
Backlash is present in most mechanical and hydraulic systems. In many cases backlash is necessary to proper work of a mechanical system. A gearbox without backlash will not work if temperature rises. The backlash in a system deacreases control performance and in most applications introduces oscillations to the controlled system.
At the beginning the backlash have to be added to existing servo system. Add this module between the inertia and the encoder modules in the system chain. It is important that encoder measures angle after backlash module.
To test behaviour of the real-time system with backlash module for different gains of the P controller click PID control continuous button in Servo Control Window. The model given in Fig. 7.1 opens. Type K=[0.1024 0 0] at the MATLAB prompt. It set proportional coefficient Kp of the P
controller. Assuming a desired range of change of the output disk equal to pi/8 set reference input signal equal to 100*pi/8 (it is the measured angle at the input to the gearbox). Also set frequency of the reference input to 0.05 Hz and sample time to 0.002 [s].
- Build the model.
- Click the Simulation/connect to target and Start real-time code options to start experiment.
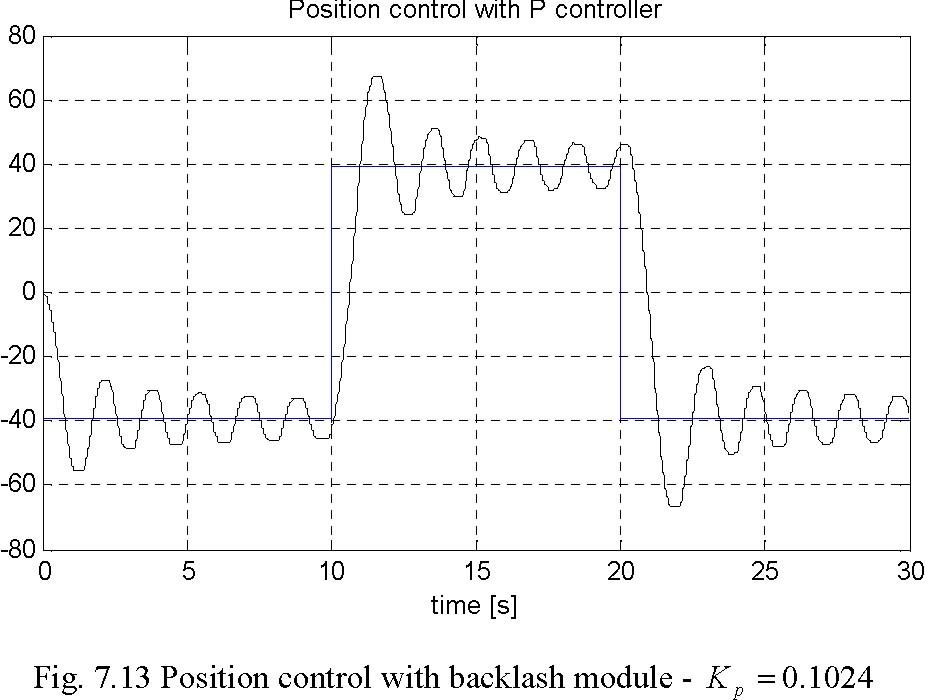
The results are given in Fig. 7.13 and Fig. 7.14.
time [s]
Notice, that oscillations in the system occur. These oscillations have nonlinear shape, significant amplitude and are result of a limit cycle in the system. The control shown in Fig.
7.14 is saturated. It is known fact that decreasing the proportional gain of the controller can correct this unfavourable behaviour of the servo system.
Controls 1
0.5
0
-0.5
-1 time [s]
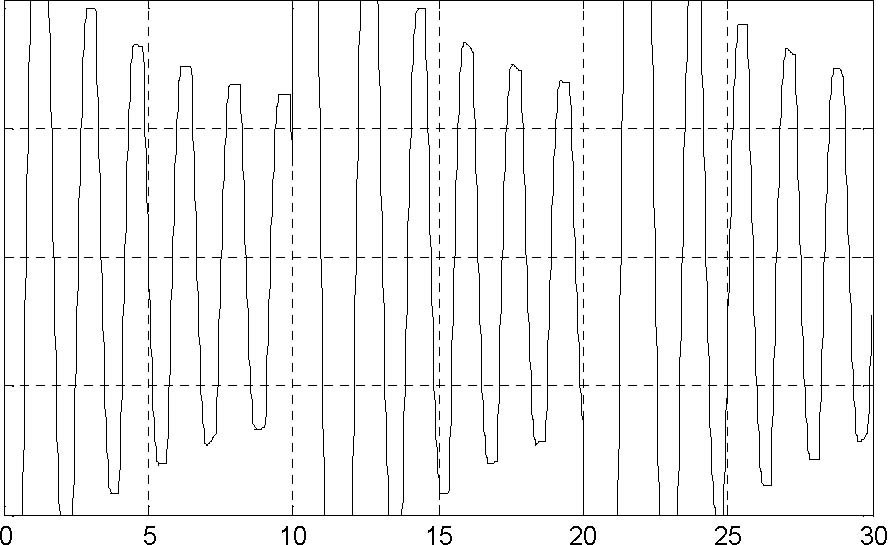
Fig. 7.14 Control signal Next repeat the experiment for Kp = 0.0128 . The results of this experiment are given in Fig.
7.15 and Fig. 7.16.
Position control with P controller 80 60 40 20 0 -20 -40 -60 time [s]
Fig. 7.15 Position control with backlash module Kp = 0.0128
One can observe that oscillations are not present in this case. The desired position is reached with 2.8% accuracy. The control saturations does not occur. It can be stated that closed-loop system behaviour is satisfactory.
Controls 1
0.5
0
-0.5
-1
time [s]
Fig. 7.16 Control signal
7.2. PID Velocity control
The task of the velocity control is keep the desired velocity in present of the disturbances. The disturbances can be introduced as a change of the velocity reference signal or as change of the motor load. To disturb the reference velocity the potentiometer can be used. The load disturbances can be introduced by braking slightly the inertia load of the system. In the example the handy load disturbances were realized.
Click the Velocity control button in Servo Control Window and model shown in Fig. 7.17 opens.
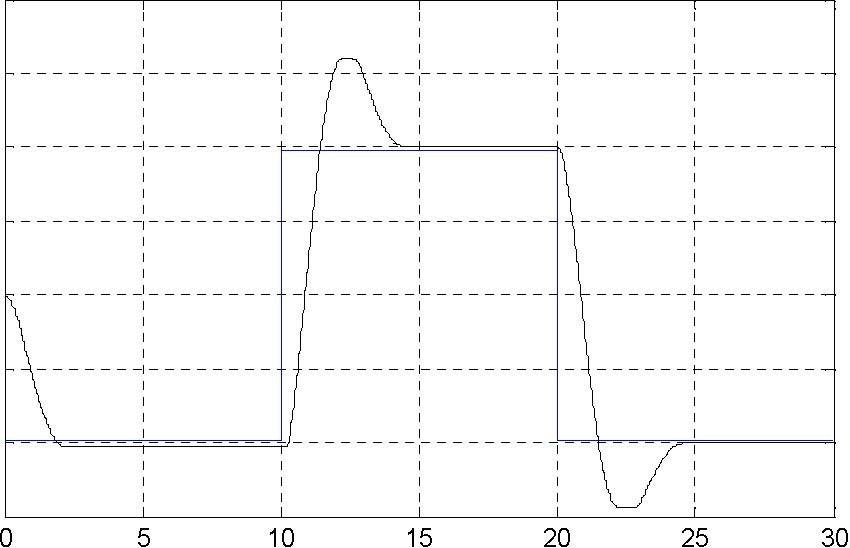
Set sine reference velocity, amplitude equal to 40 [rad/s] and frequency 0.1 [Hz] . Simulation time set 30 [s]. The Gain of the potentiometer set equal to zero. The coefficients of the PID controller set as K = 0.15 and K= 0.03 .
pi
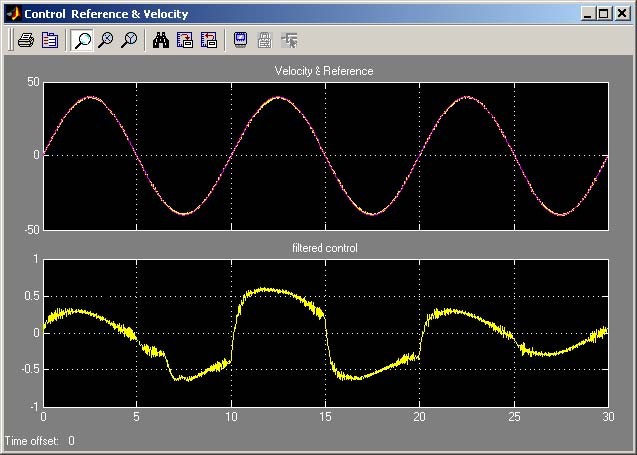
Build the model and run real time code. The results of the experiment are given in Fig.
7.18.
One can see that the disturbances of the motor load were introduced (by braking by hand the inertia load) at fifth second and finished at twentieth second. Note that the control increases in this time interval. The results are stored in VelCtrl variable placed in the Matlab workspace.
Type at the Matlab prompt :
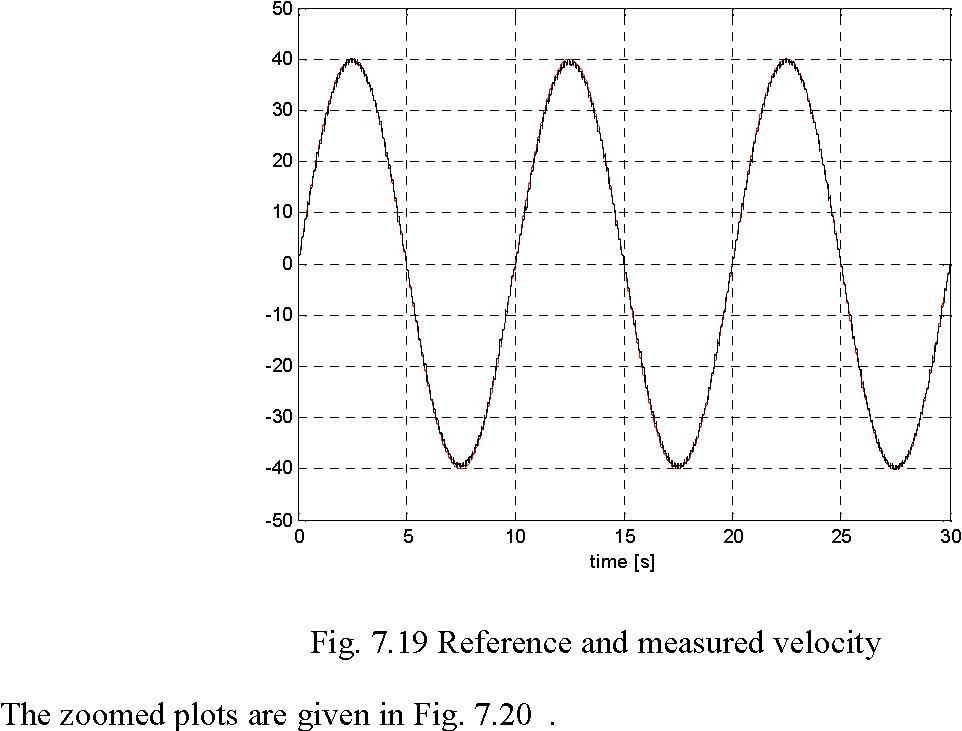
plot(VelCtrl.time,VelCtrl.signals(1).values(:,2), r ,VelCtrl.time,VelCtrl .signals(1).values(:,1), k );grid;xlabel( time [s] );title( Reference velocity (red) -measured velocity (black) );
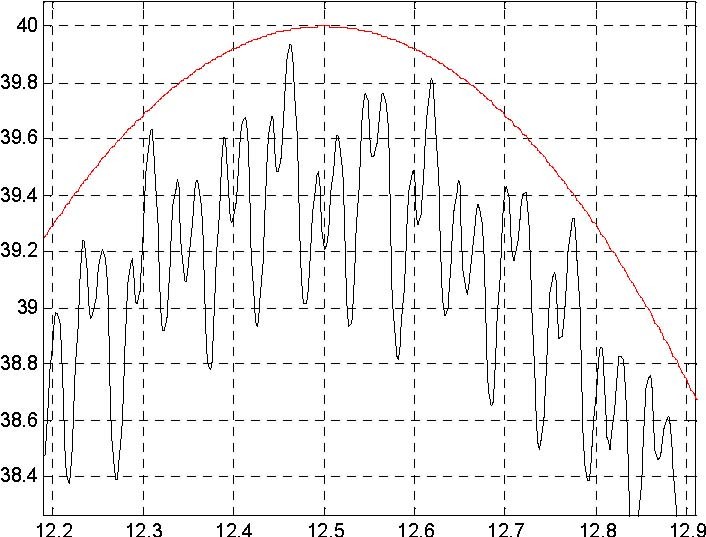
The plot is shown in Fig. 7.19 . In this scale the differences between the plots are unvisible. The details of the reference velocity and the measured velocity are shown in Fig. 7.20.
Reference velocity (red) -measured velocity (black)
time [s]
Reference velocity (red) -measured velocity (black)
time [s]
Fig. 7.20 Zoomed data
The tracking error of the velocity (at 12.5 second) is equal to 1%. Of course this error varies along the time axis but always is not large in relation to the error of the velocity measurements.
7.3. Multivariable control design
The section demonstrates how properties of a closed-loop system are influenced by the design parameters: the closed-loop roots and sampling period. Two methods of the closed-loop systems design are shown. The first is based on pole placement and is applied for continuous systems. The second control method, known as "deadbeat control" is used for discrete systems.
7.3.1. Pole-placement method
A closed-loop system with feedback gains from the states is analysed. The approach we wish to apply is a pole placement. It means that we can change the closed-loop system roots. There are different ways of achieving this. One of the design methods is described below.
The continuous-time system is represented by the state equation:
x& = Ax + Bu
y = Cx
The state controller realises a linear feedback control law in the form: u = K( yd − y),
where K is a feedback gain matrix and yd is the desired output vector.
We request that the roots of the closed system are equal to λ1,λ2 (fixed). The design methods consist in finding K that the roots of the closed-loop system are in the desired locations. That means, we assume dynamic properties of the closed system. It can be shown that there exists a linear feedback that gives a closed-loop system with roots specified if and only if the pair (A, B) is controllable. It is clear that closed-loop system has to be stable and it is a sine qua non assumption of the design.
The state matrix of the closed-loop system is
Ac = (A − BKC ).
For the case of the DC motor the matrix Acis given as
01 Kk 1+ Kk
s 1 s
⎢
⎥
Ac =
−
−
2
,
Ts Ts
and the characteristics equation has the form 1+ Kk Kk
2 s 2 s 1
λ + λ += 0.
Ts Ts
By means of the feedback gains, the location of roots of the characteristics equation may be changed. From the Vieta s formula we obtain
Kk 1+ Kk
s 1 s 2
λ ⋅ λ = (λ + λ ) =− ,
12 12
Ts Ts and we can calculate k1 and k2 from
λ ⋅ λ ⋅Ts (λ + 2)Ts +
1 2 1 λ 1
k1 = k2 =− . (7.1)
Ks Ks
It is clear that we can require a desired behaviour of the closed-loop system but we have to keep the control between appropriate limits |u(t)| ≤ 1. When the control variable saturates, it is necessary to be sure that the system behaves properly.
EXAMPLE
Assume we want to design a closed-loop system without oscillations. A possible selection of the roots is:
λ1 =−2 and λ2 =−3.
For the identified parameters (an example) Ks = 186 [rad/s] and Ts= 1.04 [s] we can
calculate k1, k2 from formula (7.1)
1 = 0.0335 and k = 0.0226
k 2
Then, we simulate the closed-loop system with feedback gains k1, k2.
Perform the following steps:
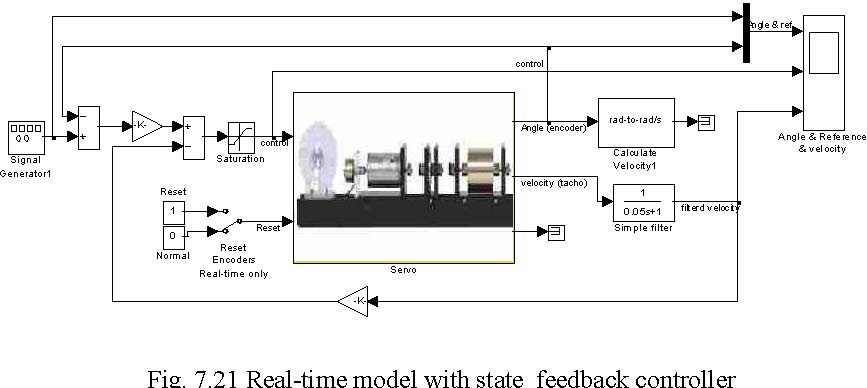
- type K=[0.0335 0.0226] and servo at the MATLAB prompt.
- Double click the State feedback control continuous and State feedback controller buttons. The model shown in Fig. 7.21 opens. Assuming a desired range of change of the output disk position equal to pi/8 set reference input signal equal to 100*pi/8 (it is the measured angle at the input to the gearbox). Also set frequency of the reference input to
0.1 Hz and sample time to 0.002.
- Build the model.
- Click the Simulation/connect to target and Start real-time code options to start the experiment.
The results are presented in Fig. 7.22. Notice, that the response of the system is slow and not
accurate. The reference angle is reached with accuracy equal to 6% and the settling time is
about 4[s].
We can change the roots of the closed-loop system to make the system faster. Assuming λ1 =−4 and λ2 =−5 we obtain: k1 = 0.1118 and k2 = 0.0449 .
State feedback controller
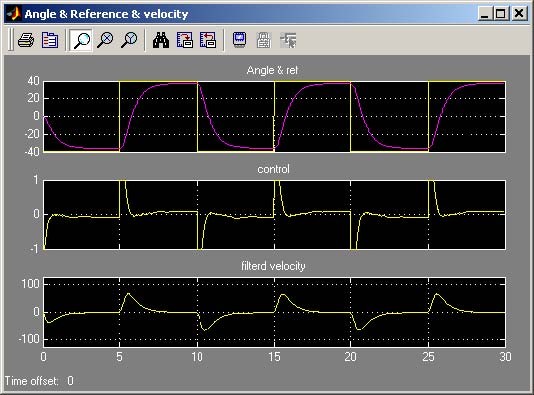
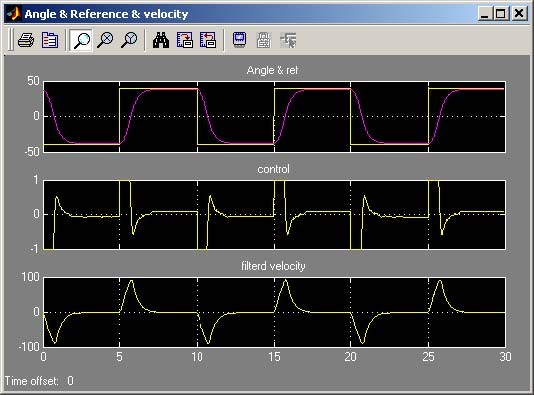
Type at Matlab prompt K=[0.0335 0.0226] and repeat the experiment with the new values of k . The experimental results are shown in Fig. 7.23. Notice that the response of the
1, k2
system is faster and more accurate. The reference angle is reached with accuracy equal to 2.3% and the settling time is 2.5 [s]. These results outperform the previous one.
In both experiments the control saturates despite that the goals of the design are achieved.
⎥⎦
7.3.2. Deadbeat controller
It is the control method unique to discrete systems in which we calculate feedback gains in such a way that roots of the closed system are equal to zero. This control strategy has the property that it drives the states of a closed-loop system from an arbitrary values to zero in at most N steps (dim(A)=N). It is the fastest possible discrete controller.
The sampling time T0 is the only design parameter. The magnitude of the control variable u can be decreased by increasing the sampling time T0, or vice versa. For a given range of the reference variable step a suitable sample time can be determined. The main problem of the design is the saturation of system actuators.
The discrete system is described by a discrete state equation:
x[( n + 1)T ] = Ax[nT ] + Bu[nT ]
0 D 0 D 0
y[nT ] = Cx[nT ].
0 D 0
The matrices ADand BD are calculated from the continuous state-space model using the following, well known, relations:
dt B
T
0
AT0 At
∫
CD CAD
=I.
B
⎢
=
=
=
e e
D
0
For a discrete model of the DC motor matrices Adand Bd have the form
Modular Servo System -User’s Manual
T
0
T
0
−−
TsTs
− S −
−
K
S
(T
(1
))
1 S (1
)
⎢
T
⎥
⎢
T
⎥
e
eAD
=
e
AT
0
=
0
,
B
D
=
.
T
0
T
0
−
−
Ts
Ts
(1 −
e
)
0
e
K
S
If we assume reachability of the pair ( AD,BD ) and a control law in the form u[( n)T ] = K( y [nT ] − y[nT ])
0 d 00
K = [k1k2], we obtain the closed-loop system shown in Fig. 7.24.
y [nT0]
yd [nT0]
x[( n +1)T ] = Ax[nT ] + Bu[nT ]
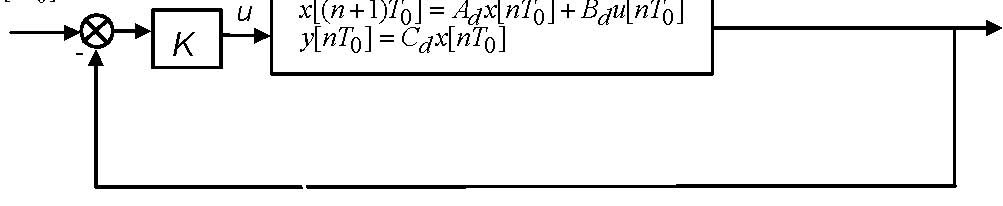 u 0 d 0 d 0
u 0 d 0 d 0
y[nT ] = Cx[nT ]
0 d 0
Fig. 7.24. Closed-loop system with the feedback gain
The closed-loop system is described by the equation
x[( n +1)T ] = (A − B KC )x[nT ] + B Ky [nT ].
0 D DD 0 Dd 0
Feedback gains for the deadbeat controller are calculated from the equation:
det( λI − (AD − BDKC D )) |λi =0,i=1,2 = 0.
Design method
We can design deadbeat controller using a simulation method. The following steps are necessary in this case:
- choose the sampling time T0,
- create a discrete model,
- calculate feedback gains,
- simulate the closed-loop discrete system,
- if the control overruns saturation limits increase the sampling time T0and repeat the steps from 1 to 5.
EXAMPLE
This example shows how to design the deadbeat controller.
A goal of the control is to track a reference signal (the angle of the motor shaft). The reference signal is assumed a square wave.
Type servo at the MATLAB prompt and then double click the State feedback control discrete button. To design the controller click the Calculate deadbeat controller button. It executes the servo_calc_db.m file where a coefficients of deadbeat controller are calculated according to algorithm shown above. The body of this file is listed below. Notice the comments in the file.
% Continuous linear model of the servo system. % Parameters of the servo are read from workspace
A=[0 1;0 -1/Ts]; B=[0; Ks/Ts]; C = [1 0;0 1]; D = zeros( 2, 1 );
% If the distance to the reference signal is big control value in the % first sample time is big too. Due to we are looking for such a T0 % when control does not saturate,we must assume the maximum change of % the reference signal.
delta_ref=[25*pi;0]; && it is maximal change of the reference signal
% we start look for T0 T0=0.1; for i = 1:200 T0=T0+0.005;
% ** Discrete model for sampling time T0*
[Ad,Bd]=c2d(A,B, T0);
% Now we calculate a coeffitients of deadbeat controller % using the formula : eig(Ad-Bd*K)=0
Z=[Bd(1) Bd(2); Ad(2,2)*Bd(1)-Ad(1,2)*Bd(2) Ad(1,1)*Bd(2)]; X=[Ad(1,1)+Ad(2,2);Ad(1,1)*Ad(2,2)]; K=(Z\X) ;
% Now coefficients of the controller are saved in K
% checking if the control saturates in the first sample time: % u(1)=K*delta_ref;
if abs(K*delta_ref)<=1 K T0 && write K and T0 in Matlab command window return end end
The variables K and T0are stored in the MATLAB workspace after the execution of the
above m-file. In our case for Ks = 186 [rad/s] and Ts= 1.04 [s] we obtain
K = [0.0127 0.0091] and T0 = 0.7950 . Now double click the State feedback controller buttons to perform the real-time experiment and the model depicted in Fig. 7.25 opens.
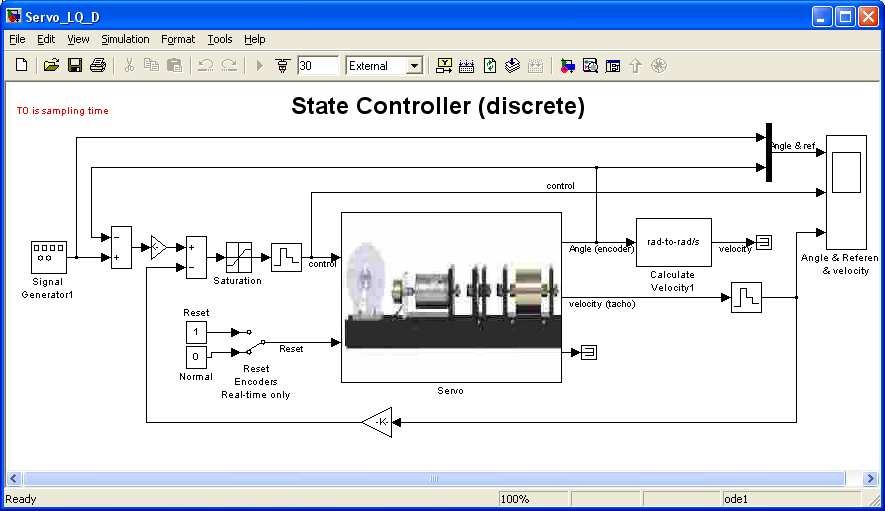
This model differs in details from the other models. Due to the fact that the model is discrete, and the sampling time T0can vary from experiment to experiment T0is read from
the Matlab workspace. Variable T0is located in the Simulink model in the following places: in Fixed step size in tag Solver which is located in Simulation/Simulation Parameters option, in all Zero-Order Hold blocks and in the mask of the Servo device driver. There is no filter connected to the output of the tachogenerator. The filter applied in other models is not discrete one and can not be used here. However it is interesting how the controller works without filtering of the velocity signal.
Set the amplitude of the input signal to 100*pi/8 (as in the previous example), the frequency of reference signal to 0.05 Hz. Set simulation time equal to 60 [s] and time range in the scope also 60 [s]
Due to the fact that the model includes variables K and T0and some settings was changed rebuild it. Click Simulation/connect to target. Click the Start real-time code option to start the experiment. The results are shown in Fig. 7.26.
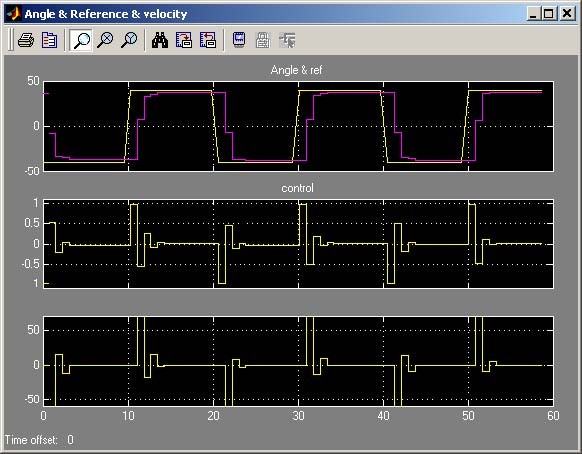
Note, that the system does not reach the reference angle in two steps. In fact, the servo is a nonlinear system and it is only approximated by a linear model. Notice that this control is significant only during two first sample intervals.
7.4. Optimal design method: LQ controller
The linear-quadratic problem (LQ problem) is a central one in the theory and applications of optimal control. There are two versions of the LQ problem: the open-loop and the closed-loop optimal control problems. Either the optimal control is given as an explicit function of time for fixed initial conditions, or the optimal controller is synthesised. Further only the second case is considered. The main result of the finite-dimensional linear-quadratic theory is that under suitable assumptions the optimal feedback controller is linear with respect to the state, and constant with respect to time.
The synthesis of the discrete and continuous LQ controller is presented below. For a very small value of the sampling time the response of the discrete system converges to the response of the corresponding continuous system. The most important question for a designer of a control system, as far as LQ control problem is concerned, is how to select the weighting factors in the cost function.
Let us examine separately the continuous and discrete LQ problems.
7.4.1. The continuous case
The dynamical model of the DC-motor is described by the linear differential equations:
x& = Ax + Bu
y = Cx ,
where the matrices A, B and C have the form
⎡01 ⎤ 0 ⎡10⎤
A = 1 ⎥, B = Ks ⎥, C = . (7.2)
0 − ⎢01⎥
⎥⎢⎥⎣⎦
TT
S ⎦ S
The desired input time history of the state vector is given by y (t) = [ y (t), y (t)] .
d 1d 2d
Hence, the error vector e is defined
e(t) = yd (t) − y(t).
A typical quadratic cost function (performance index) has the form
Tk
J (u) = 12 ∫[eT (t)Qe (t) + uT (t)Ru (t)] dt ,
0
where:
- matrix Q ≥ 0, Q is a nonnegative definite matrix,
- matrix R > 0, R is a positive definite matrix,
- the (A,B) pair is controllable.
The weighting matrices Q and R are selected by a designer but they must satisfy the above conditions. It is most easily accomplished by picking the matrix Q to be diagonal with all diagonal elements positive or zero. Some positive weight (|R|≠0) must be selected for the control, otherwise the solution will include infinite control gains.
The values of elements of Q and R matrices weakly correspond to the performance specification. A certain amount of trial and error is required with a simulation program to achieve satisfactory result. A few guidelines can be recommended. For example, if all states are to be kept under close regulation and Q are diagonal with entries so selected that a fixed percentage change of each variable makes an equal contribution to the cost. The matrix R is also diagonal.
If the maximum deviations of the servomechanism outputs are: , and the
y1max y2 max
maximum deviation of control is umax , then the cost is:
2 22
Q( 1,1)y 1 + Q( 2,2 )y 2 + Ru
The coefficients of the Q and R matrices can be set related to the rule: 1 11
Q(1,1) = 2, Q(2,2) = 2 and R = 2
( y )( y )(u )
1max 2max max
This rule can be modified to satisfy desired root locations and transient response for selected values of weights. One must avoid saturation effects both of outputs and control.
Due to the differences in methods of analysis, problem formulation and the form of results, we strongly distinguish the linear-quadratic problem with a finite settling time from that with a infinite settling time. However in applications we frequently encounter the situation when the termination moment of the control process is so far away that it does not affect the current control actions. The infinite-time optimal control problem is then posed. The cost function is replaced by the formula:
∞
J (u) = ∫[eT (t)Qe (t) + uT (t)Ru (t)] dt (7.3)
0
Then the optimal scalar control u * and the optimal trajectory vector y *are given
u * = K( yd − y *) (7.4)
where K is the feedback matrix.
The optimal control problem is now defined as follows: find the gain K such that the feedback law (7.4) minimises the cost function (7.3) subject to the state equation (7.2). The calculation of the control variable which minimizes the criterion (7.3) is a dynamic optimisation problem. This problem can be solved by variation calculus applying the maximum principle due to the Bellman optimisation principle. The procedure returns the optimal feedback matrix K, the matrix S, the unique positive definite solution to the associated matrix Riccati equation:
SA + ATS -SBR-1BTS + Q = 0
Due to the quadratic appearance of S, there is more than one solution, and S must be positive definite to select the correct one. The procedure returns also the matrix E, the closed-loop roots:
E = eig(A -B*K*C)
The vector K can be calculated by a numeric iterative formula on the basis of the Riccati equation. The associated closed-loop system e& = (A − BKC )e is asymptotically stable.
To solve the LQ controller problem the lqry function from the Control System Toolbox can be used. The synopsis of lqry is: [K,S,E] = lqry(A,B,C,D,Q,R).
In this case the matrix of weights Q relate the outputs y instead of the state x. For the servomechanism D is the row matrix with two zero elements. The function lqry computes the equivalent Q, R and calls lqr,
The control u is not constrained. This assumption can not be satisfied for a real physical system. One must remember that if the control u saturates then it not satisfies the LQ problem. To return to the LQ problem the amplitude of the u signal should be diminished. In such a case a designer tunes the relative weights between state and control variables. To perform that the simulation tools are recommended.
EXAMPLE
The goal of the control is to track a reference signal which is defined as a square wave. Set the amplitude of the reference input signal equal to 100*pi/8. Set the frequency of the reference input to 0.1 Hz and sample time to 0.002 [s].
Type servo at the MATLAB prompt and then double click the State feedback control continuous button. To design LQ controller click the Calculate LQ controller button. It executes servo_calc_lq.m file presented below:
% State space representation of servo: A=[0 1;0 -1/Ts]; B=[0; Ks/Ts]; C = [1 0;0 1]; D = zeros( 2, 1 );
% Set Q and R matrices. These values can be changed by a user Q=[50 0;0 1]; R=1000;
% calculate coefficients of the LQ controller [K,S,lambda]=lqry(A,B,C,D,Q,R);
% type K in Matlab command window K
For the default values: Ks = 186 [rad/s] and Ts= 1.04 [s] we obtain K = [0.2236 0.054] .
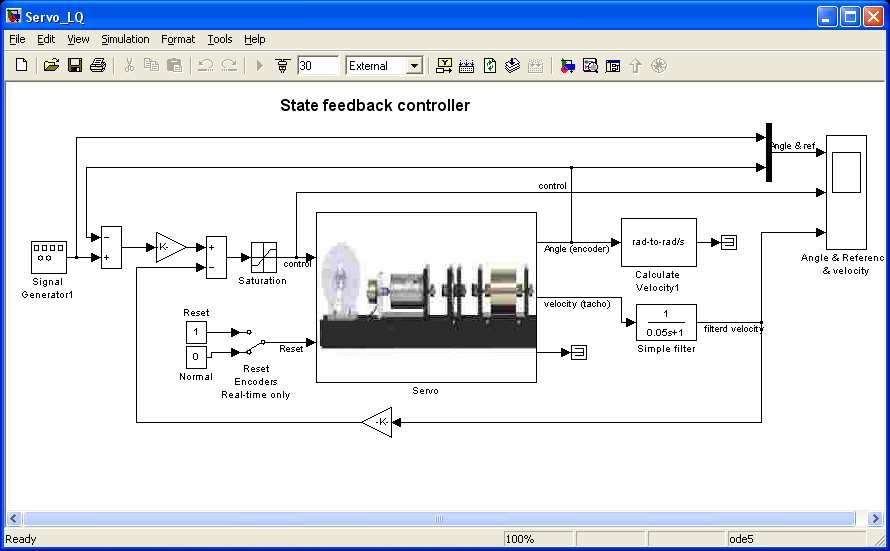
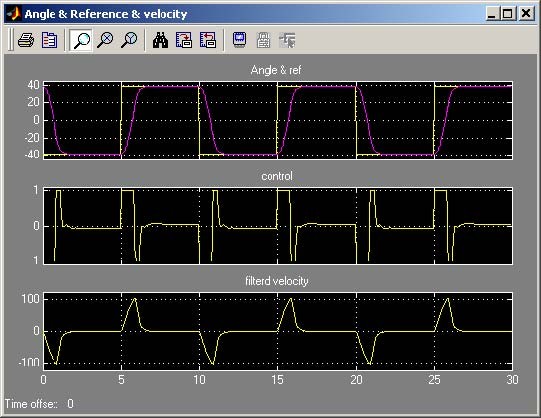
To perform the real-time experiment click the State feedback controller button. When the model opens (see Fig. 7.27), check parameters of the reference signal. Build the model, click Simulation/connect to targetand Start real-time code option to start experiment. The results are given in Fig. 7.28. Notice that the reference signal is reached with accuracy equal to 0.58% and without overshoots. The control signal saturates.
7.4.2. The discrete case
If we introduce the sampling period T0then the model can be discretized. The discrete model of the DC motor has the form:
x[( n + 1)T ] = Ax[nT ] + Bu[nT ]
0 D 0 D 0
(7.5)
y[nT ] = Cx[nT ].
0 D 0
where the matrices: AD, BD and CD are in the form
T
0
T
0
−−
TsTs
− S −
−
K
S
(T
(1
))
1 S (1
)
⎢
T
⎥
⎢
T
⎥
ee
AD
=
e
AT
0
=
0
,
B
D
=
.
T
0
T
0
−−
TsTs
(1 −
e
)
0
e
K
S
The matrix ADis the fundamental solution of the differential equation (7.5) calculated for the sampling period T0. The explicit values of the matrices ADand BD of the servo system can be obtained numerically by the use ofc2d function. C2d converts a continuous state representation to the discrete corresponding to the continuous. The procedure is a part of Control System Toolbox. One must simply type the command:
[ AD,BD ]=c2d(A,B, T0)
The optimal feedback law:
u[nT ] = Ke [nT ], e[nT ] = y − y[nT ]
0 00 d 0
minimizes the cost function:
N
J (u)
=
∑
[
e
T (n)Q(n)e(n) uT (n)Ru (n)] (7.6)
+
n=0
subject to the state equation (7.5). The dlqry function from the Control System Toolbox is used to solve the discrete-time linear-quadratic control problem. The synopsis of the dlqry and lqry programs are identical. The dlqr also solves and returns matrix S, the unique positive definite solution to the associated discrete iterative matrix Riccati equation:
TT T −1 T
S = ASA − A SB (R + B SB ) B SA + Q .
i+1 DiD DiD DiD DiD
The feedback matrix is derived from S by
T − T
K = (R + B SB )1 B SA
DD DD
EXAMPLE
A goal of the control is the same as in the continuous case example. Assume that sampling time for discrete system T0 = 0.1[s].
In Servo Control Window double click the State feedback control discrete button. To design the LQ controller click the Calculate LQ controller button. It executes the servo_calc_lq_d.m file presented below.
% State space representation of servo: A=[0 1;0 -1/Ts]; B=[0; Ks/Ts]; C = [1 0;0 1]; D = zeros( 2, 1 );
% set sampling time T0=0.1; % calculate discrete model from continuous [Ad,Bd]=c2d(A,B, T0)
% set Q and R matrices Q=[50 0;0 1]; R=1000;
% design discrete LQ controller
[K,S,lambda]=dlqry(Ad,Bd,C,D,Q,R); K
For the default values: Ks = 186 [rad/s] and Ts= 1.04 [s] we obtain K = [0.139 0.0395] .
To perform the real-time experiment click the State feedback controller button and the model shown in Fig. 7.25 opens. It is the same model as are previously applied to deadbeat control. Set the frequency of the reference signal to 0.1 [Hz] the simulation time to 30 [s] and the time range of the scope to 30 [s]. These settings correspond to the values which have been assumed for the continuous LQ controller. Build model, click theSimulation/connect to target and the Start real-time code options to start experiment.
The results are shown in Fig. 7.28. They are similar to these for the continuous controller. The reference signal is reached with accuracy equal to 1% and without overshoots. The control signal saturates as in the previous example.
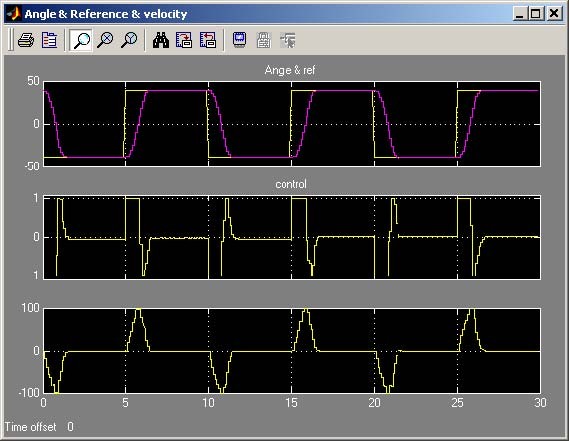
8. Description of the Modular Servo class properties
The CServo is a MATLAB class, which gives the access to all the features of the RT-DAC4/PCI board supported with the logic for the MSS model. The RT-DAC4/PCI board is an interface between the control software executed by a PC computer and the power-interface electronic of the modular servo model. The logic on the board contains the following blocks:
- incremental encoder registers – two 32-bit registers to measure the position of the incremental encoders. There are two identical encoder inputs, that may be applied to measure the shaft positions of two modular servo blocks;
- incremental encoder reset logic. The incremental encoders generate different output waves when the encoder rotates clockwise and counter-clockwise. The encoders are not able to detect the reference (“zero”) position. To determine the “zero” position the incremental encoder registers have to be set to zero by the computer program;
- PWM generation block – generates the Pulse-Width Modulation output signal. Simultaneously the direction signal and the brake signal are generated to control the power interface module. The PWM prescaler determines the frequency of the PWM wave;
- power interface thermal flags –the thermal flags can be used to disable the operation of the overheated DC motor;
- interface to the on-board analog-to-digital converter. The A/D converter is applied to measure the position of the external potentiometer and to measure the output voltage of the tachogenerator.
All the parameters and measured variables from the RT-DAC4/PCI board are accessible by
appropriate properties of the CServo class. In the MATLAB environment the object of the CServo class is created by the command: object_name = CServo; The get method is called to read a value of the property of the object: property_value = get( object_name, ‘property_name’ ); The set method is called to set new value of the given property: set( object_name, ‘property_name’, new_property_value ); The displaymethod is applied to display the property values when the object_name is entered in the MATLAB command window.
This section describes all the properties of the CServo class. The description consists of the following fields:
| Purpose | Provides short description of the property |
| Synopsis | Shows the format of the method calls |
| Description | Describes what the property does and the restrictions subjected to the property |
| Arguments | Describes arguments of the set method |
| See | Refers to other related properties |
| Examples | Provides examples how the property can be used |
8.1. BaseAddress
Purpose: Read the base address of the RT-DAC4/PCI board.
Synopsis: BaseAddress = get( sv, ‘BaseAddress’ );
Description: The base address of RT-DAC4/PCI board is determined by computer. Each CServo object has to know the base address of the board. When a CServo object is created the base address is detected automatically. The detection procedure detects the base address of the first RT-DAC4/PCI board plugged into the PCI slots.
Example: Create the CServo object:
sv = CServo;
Display their properties by typing the command:
sv
Type: CSERVO Object BaseAddress: 54272 / D400 Hex Bitstream ver.: x402 Encoder: [ 0 46606 ][bit] Reset Encoder: [ 0 0 ] Input voltage: [ 0.1123 0.1123 ][V] PWM: [0] PWM Prescaler: [ 0 ] Thermal status: [ 0 ] Thermal flag: [ 1 ] Angle: [ 0 71.4927 ][rad] Time: 31.657 [sec]
Read the base address: BA = get( sv, ‘BaseAddress’ );
8.2. BitstreamVersion
Purpose: Read the version of the logic stored in the RT-DAC4/PCI board.
Synopsis: Version = get( sv, ‘BitstreamVersion’ );
Description: The property determines the version of the logic design of the RT-DAC4/PCI board. The modular servo models may vary and the detection of the logic design version makes it possible to check if the logic design is compatible with the physical model.
8.3. Encoder
Purpose: Read the incremental encoder registers.
Synopsis: enc = get( sv, ‘Encoder’ );
Description: The property returns two digits. They are equal to the number of impulses generated by the corresponding encoders. The encoder counters are 32-bit numbers so the values of this property is from (–231) to (231-1). When an encoder counter is reset the value is set to zero. The incremental encoders generate 4096 pulses per rotation. The values of the Encoder property should be converted into physical units.
See: ResetEncoder, Angle, AngleScaleCoeff
8.4. Angle
Purpose: Read the angle of the encoders.
Synopsis: angle_rad = get( sv, ‘Angle’ );
Description: The property returns two angles of the corresponding encoders. To calculate the angle the encoder counters are multiplied by the values defined as the AngleScaleCoeff property. The angles are expressed in radians.
See: Encoder, AngleScaleCoeff
8.5. AngleScaleCoeff
Purpose: Read the coefficients applied to convert the encoder counter values into physical units.
Synopsis: scale_coeff = get( sv, ‘AngleScaleCoeff’ );
Description: The property returns two digits. They are equal to the coefficients applied to convert encoder impulses into radians. The incremental encoders generate 4096 pulses per rotation so the coefficients are equal to 2*pi/4096.
See: Encoder, Angle
8.6. PWM
Purpose: Set the direction and duty cycle of the PWM wave.
Synopsis: PWM = get( sv, ‘PWM’ ); set( sv, ‘PWM’, NewPWM );
Description: The property determines the duty cycle and direction of the PWM wave. The PWM wave and the direction signals are used to control the DC drive so in fact this property is responsible for the DC motor control signal. The NewPWM variable is a scalars in the range from –1 to 1. The value of –1, 0.0 and +1 mean respectively: the maximum control in a given direction, zero control and the maximum control in the opposite direction to that defined by –1.
The PWM wave is not generated if the thermal flag is set and the power amplifier is overheated.
See: PWMPrescaler, Therm, ThermFlag
Example: set( sv, ‘PWM’, [ -0.3 ] );
8.7. PWMPrescaler
Purpose: Determine the frequency of the PWM wave.
Synopsis: Prescaler = get( sv, ‘PWMPrescaler’ ); set( sv, ‘PWMPrescaler’, NewPrescaler );
Description: The prescaler value can vary from 0 to 63. The 0 value generates the maximal PWM frequency. The value 63 generates the minimal frequency. The frequency of the generated PWM wave is given by the formula:
PWMfrequency = 40MHz / 1023 / (Prescaler+1)
See: PWM
8.8. Stop
Purpose: Sets the control signal to zero.
Synopsis: set( sv, ‘Stop’ );
Description: This property can be called only by the set method. It sets the zero control of the DC motor and is equivalent to the set(sv, ‘PWM’, 0) call.
See: PWM
8.9. ResetEncoder
Purpose: Reset the encoder counters.
Synopsis: set( sv, ‘ResetEncoder’, ResetFlags );
Description: The property is used to reset the encoder registers. The ResetFlags is a 1x2 vector. Each element of this vector is responsible for one encoder register. If the element is equal to 1 the appropriate register is set to zero. If the element is equal to 0 the appropriate register counts encoder impulses.
See: Encoder
Example: To reset only the first encoder register execute the command: set( sv, ‘ResetEncoder’, [ 1 0 ] );
8.10. Voltage
Purpose: Read two voltage values.
Synopsis: Volt = get( sv, ‘Voltage’ );
Description: Returns the voltage of two analog inputs. Usually the analog inputs are applied to measure the position of the external potentiometer and the output of the tachogenerator.
8.11. Therm
Purpose: Read thermal status flag of the power amplifier. Synopsis: Therm = get( sv, ‘Therm’ ); Description: Returns the thermal flag of the power amplifier. When the temperature of a
power amplifier is too high the flag is set to 1.
See: ThermFlag
8.12. ThermFlag
Purpose: Control an automatic power down of the power amplifiers.
Synopsis: ThermFlag = get( sv, ‘ThermFlag’ ); set( sv, ‘ThermFlag’, NewThermFlag );
Description: If the ThermFlag or NewThermFlag are equal to 1 the DC motor is not excited by the PWM wave when the power interface is overheated.
See: Therm
8.13. Time
Purpose: Return time information.
Synopsis: T = get( sv, ‘Time’ );
Description: The CServo object contains the time counter. When a CServo object is created the time counter is set to zero. Each reference to the Time property updates its value. The value is equal to the number of milliseconds which elapsed since the object was created.
8.14. Quick reference table
| Property name | Operation* | Description |
|---|---|---|
| BaseAddress | R | Read the base address of the RT-DAC4/PCI board |
| BitstreamVersion | R | Read the version of the logic design for the RT-DAC4/PCI board |
| Encoder | R | Read the incremental encoder registers |
| Angle | R | Read the angles of the encoders |
| AngleScaleCoeff | R | Read the coefficient applied to convert encoder positions into radians |
| PWM | R+S | Read/set the parameters of the PWM waves |
| PWMPrescaler | R+S | Read/set the frequency of the PWM waves |
| Stop | S | Set the control signal to zero |
| ResetEncoder | R+S | Reset the encoder counters or read the reset flags |
| Voltage | R | Read the input voltages |
| Therm | R | Read the thermal flags of the power amplifiers |
| ThermFlag | R+S | Read/set the automatic power down flag of the power amplifier |
| Time | R | Read time information |
• R – read-only property, S – allowed only set operation, R+S –property may be read and set
8.15. CServo Example
To familiarise a reader with the CServo class this section presents an M-file example that uses the properties of the CServo class to measure the static characteristics of the DC motor (see section 6). The static characteristics is a diagram showing the relation between DC motor control signal and the motor shaft velocity. The M-file changes the control signal and waits until the MSS reaches steady-state. The velocity of the shaft is obtained in two ways:
- the M-file measures the output voltage from the tachogenerator,
- the M-file measures the encoder position in two time points and calculates the velocity as the difference of positions divided by the time period between the time points.
The M-file is written in the M-function form. The name of the M-function is Servo_PWM2RPM.
The function requires two parameters:
- CtrlDirection -a string that selects how to change the control value. The A string causes the control is changed in ascending manner (from -1 to 1), the D string causes the control is changed in descending order (from 1 to -1) and the R string causes reverse double changes (from -1 to +1 and after that from +1 to -1),
- MinControl, MaxControl – minimal and maximal control signal values. The control signal changes within the region defined by these values,
- NoOfPoints -number of characteristics points within the MinControl/MaxControl range. The exact number of points of the characteristics declared by this parameter is enlarged to two points namely: MinControland MaxControl.
The body of this function is given below. The comments within the function describe the main stages.
function ChStat = Servo_PWM2RPM( … CtrlDirection, MinControl, MaxControl, NoOfPoints )
CtrlDirection = lower( CtrlDirection ); NoOfPoints = max( 1, NoOfPoints+1 );
% Calculate control step Step = (MaxControl-MinControl) / NoOfPoints;
switch CtrlDirection case a Ctrl = MinControl:Step:MaxControl; case d Ctrl = MaxControl:-Step:MinControl; case r Ctrl = [ MinControl:Step:MaxControl MaxControl:-Step:MinControl]; otherwise % This should not happen error( The CtrlDirection must be A , D or R . ) end
FigNum = figure( Visible , on , ... NumberTitle , off , ... Name , Velocity vs. PWM characteristic , ... Menubar , none );
sv = cservo; Control = []; VelEnc = []; % Optionally set the PWM prescaler %set( sv, pwmprescaler , 20);
for i=1:length(Ctrl)
% Set a new control value
set( sv, PWM , Ctrl(i) );
% Reset encoders
set( sv, ResetEncoder , [1 1] );
set( sv, ResetEncoder , [0 0] );
pause( 5 )
AuxEnc = get( sv, Encoder ); TimeBeg=gettime;
pause( 2 )
% Calculate velocity based on the encoder positions
VelEnc(i,:) = 2*pi*(get( sv, Encoder )-AuxEnc)/ …
4096/((gettime-TimeBeg)/1000); % [rad/s]
Control(i) = get( sv, PWM );
Volt(i,:) = get( sv, Voltage );
% Perform 10000 A/D conversions and calculate average values
AuxVolt = [0 0];
for j=1:10000
AuxVolt = AuxVolt + get( sv, Voltage );
end
Volt(i,:) = AuxVolt/10000;
% Convert voltage into velocity
Volt2Vel = 20.4*Volt(:,2);
% Plot data
subplot(211);
plot( Control, VelEnc(:,2), Control, VelEnc(:,2), x ); grid
title( Encoder velocity vs. PWM );
xlabel( PWM control value ); ylabel( Velocity [rad/s] );
subplot(212);
plot( Control, Volt2Vel, Control, Volt2Vel, x ); grid
title( Tacho velocity vs. PWM );
xlabel( PWM control value ); ylabel( Tacho velocity [rad/s] ); end % Assign data to the structure returned by the function ChStat.Control = Control;ChStat.TachoVelocity = VelEnc(:,2); ChStat.EncoderVelocity = Volt2Vel;
% Switch off the control set( sv, Stop );
The diagrams generated by the call
servo_pwm2rpm( r ,-0.5,0.5,19),
are shown below. The diagrams present the velocity of the shaft as function of the control signal. The control signal changes from –0.5 to +0.5. The velocity value is obtained in two ways. At the upper diagram the velocity is calculated from the encoder positions. The lower diagram presents the velocity obtained from the tachogenerator.
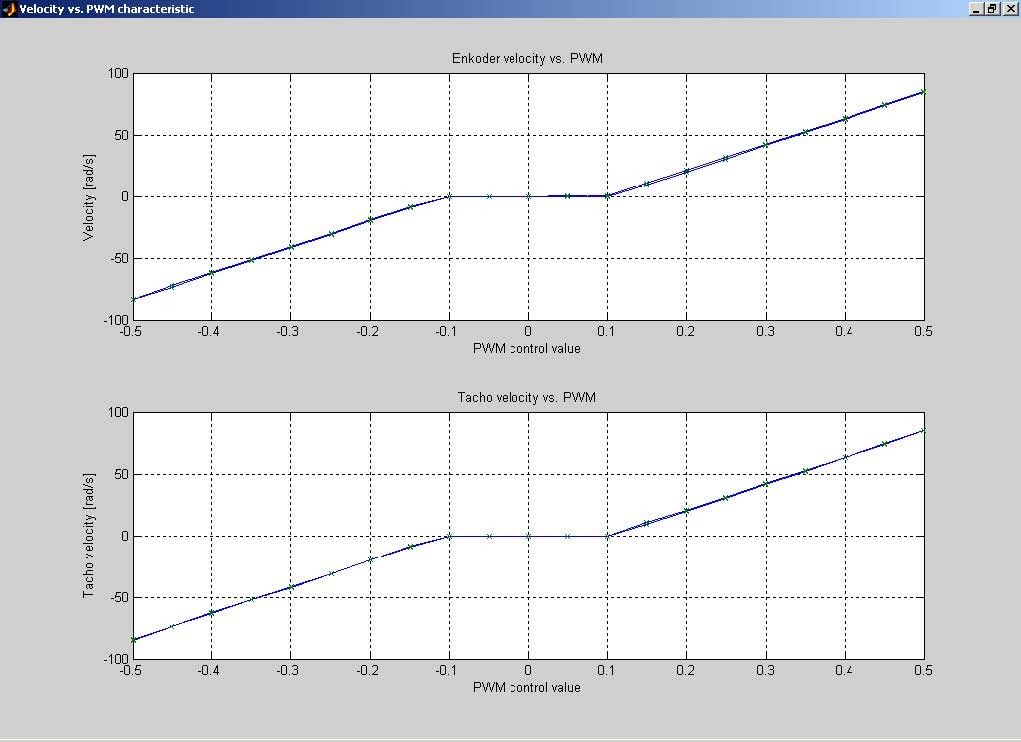
The values on the diagram may vary from experiment to experiment as they depend on the configuration of the modular servo set-up.
9. Some technical data
| 15 | Φ 20 68 Φ 66 | Φ 25 5 5 Φ 66 8,5 | Φ 20 |
| Brass inertia load 2.030 kg | 0.055 kg Aluminium wheels | 0.05 kg |
Data sheet of the DC motor
 is available at
is available at
http://www.buehlermotor.com/cgi-bin/sr.exe/productpageus&productpage=54
The gearbox ratio N = 100
url: http://www.51lm.cn/p/templates/cn/show.php?cid=905&aid=3299


