基于MATLAB的磁悬浮控制系统的研究

系统介绍

磁悬浮系统是一个典型的非线性系统，当前绝大多数磁悬浮控制器都是基于非线性磁悬浮系统在某个平衡点的线性化模型而设计的线性控制律。当系统的平衡点改变时，系统的动态特性会显著

改变。

Magnetic Levitation system is a typical nonlinear system. The current vast majority of controllers which belongs to nonlinear magnetic levitation system are based on a linear equilibrium model to design for the linear control law. When the equilibrium point of the system 改变s, the dynamic characteristics  of  the system will 改变 significantly.

磁悬浮系统是利用电磁力来控制刚体悬浮的空间位置。其工作原理是控制电磁铁绕组的电流，产生与刚体重量等价的电磁力，使得刚体稳定悬浮在平衡位置。由于电磁力与悬浮气隙间存在非线性反比关系，这种平衡并不稳定，一旦受到外界干扰(如电压脉动或者风)，刚体就会掉下来或被吸上去，因此必须实行闭环控制。

Magnetic Levitation system uses electromagnetic force to control the suspended spatial position of the rigid body. Its working principle is to control the electric current of  Electromagnet windings to produce electromagnetic force which is equivalent to the  weight of the rigid body, making the rigid body suspended in stable equilibrium position. Due to the nonlinear inverse relationship between the electromagnetic force  and Suspended air , this balance is not stable.In the event of outside interference (such as voltage fluctuation or wind), rigid body will fall off or suck up.So it is necessary to implement closed-loop control.

采用位置传感器在线获取刚体位置信号，控制器对位移信号进行处理产生控制信号，功率放大器根据控制信号产生所需电流并送往电磁铁，电磁铁产生相应磁力克服重力使得刚体稳定在平衡点附近。

With online access to the location position of the rigid body by the use of sensor signal, controller produce control signal through displacement signal processing.And the power amplifier  generate the required current according to control signals and sent to electromagnets which make  corresponding magnetic  to overcome gravity ,resulting in the stability  of rigid body  in the equilibrium point.

磁悬浮由于其无接触的特点避免了物体之间的摩擦和磨损，能延长设备的使用寿命，改善设备的运行条件，因而在交通、冶金、机械、电器、材料等各个方面有着广阔的应用前景。

Magnetic Levitation system can avoid friction and wear between the object due to its non-contact characteristics. It can also extend the Service life of equipment and improve operating conditions of the equipment. So it has broad application prospects in the transportation, metallurgy, machinery, electrical, materials and 其他 aspects.

模型介绍

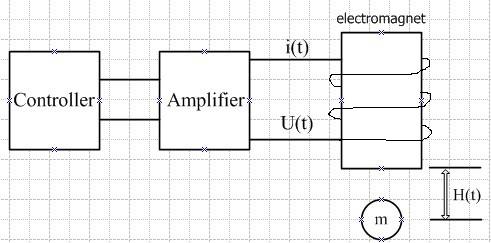
控制对象是铁磁性材料做成的球体．球的高度为h(t)，线圈电流为i(t)．磁悬浮动力学方程以及线圈回

路电压方程分别为：

Control object is a sphere made of ferromagnetic material. Ball height h (t), coil current i (t). Maglev kinetic equations and magnetic circuit voltage equations :

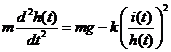
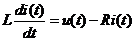                           (1)

其中m为球的质量，g为重力加速度，L为线圈电感，R为线圈电阻，k为磁场和球之间的耦合系数．系

统的输入为线圈电压u(t)，输出为球的高度h(t)．

Where m is the ball quality, g is acceleration due to gravity, L is the coil inductance, R is the coil resistance, k is the coupling coefficient between magnetic field and the ball.The  System input is Coil voltage u (t), output  the height of the ball h (t).

球与电磁铁间保持适当的距离时，电磁吸引力与重力平衡．如果球的高度下降太多，则磁场的作用力变弱而使球落下去．如果球离磁铁太近，则磁场作用又会太强而将球拉向磁铁，这也将破坏系统的稳定性。

When there is an appropriate distance between the ball and electromagnet, the magnetic attraction and gravity balanced. If the height of the ball drop too much, the force of magnetic field become weak leaving the ball drop. If the ball is too close to the the magnet ,magnetic field will be too strong and the ball will be pulled to the magnet, which will also undermine the stability of the system.

假定球的期望高度为h。，该位置称为平衡点，此处重力和电磁吸引力相等．令加速度为零，求出维持该位置的期望电流．

Assume that the expectation height of the ball is h。, the location known as the equilibrium point, where gravity and magnetic attraction are equal. So acceleration is zero, find the expectation current of maintaining this position. Namely,

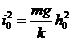
方程(1)为非线性方程．将模型在平衡点附近线性化，产生一组线性方程 ．为此引入状态变量：

Equation (1) is non-linear equation. Making the model is linearized around an equilibrium point, resulting in a set of linear equations. So introduct state variables:

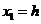
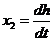
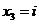
则方程(1)变为：

The equation (1) becomes:

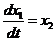
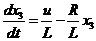
将方程(2)在工作点 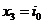, 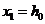处通过泰勒级数展开进行线性化，结果为：

The equation (2) unfold at the operating point 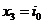, 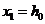by the Taylor series expansion for linearization, the result is:

控制器设计

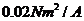假设球的质量为0．1 kg，线圈的电阻为l0 ，线圈电感为100 mH，耦合系数为，期望高度为10 cm．在MATLAB中建立系统的状态空间模型MagLev．

Assuming the quality of the ball is 0．1 kg，resistance of the coil is 10，Coil inductance is 100mh，Coupling coefficient is 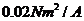，expected heigh is 10cm. Create the state space model of the system in MATLAB, MagLev.

然后求出系统极点。

Then find the system poles.

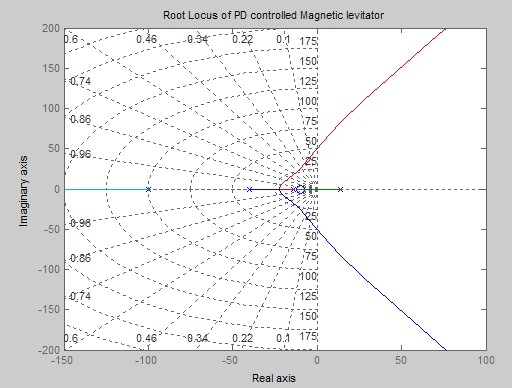
线性化后悬浮系统的极点为±14，放大器的极点为-100．需加一个PD(比例微分)控制器来稳定系统．理论上PD控制器的传递函数可写成如下形式：

After linearization the pole of the suspension system is ± 14, the pole of the amplifier is -100.  Add a PD (proportional derivative) controller to stabilize the system. In theory ,transfer function of the PD controller theory can be written as follows:

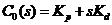
其中为比例增益，为微分增益．由于高频噪声的影响，使得微分控制难以实现，实际应用中微分作用可以近似，并通过滤波消除噪声的影响．实际控制器的传递函数形式为：

Where  is the proportional gain, is differential gain. It is difficult to achieve differential control Since high-frequency noise. The role of the differential can be approximated in the practical application. Eliminating noise by filtering. The transfer function form of the actual controller:

传递函数等价于一个超前控制器，其零点的时间常数为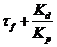，极点(滤波器)的时间常数为 ，可见零点比极点慢．选择控制器零点在系统第一个稳定极点的右侧，此处取-10，滤波器的时间常数为25 ms，极点为-40．控制器的传递函数为：

The transfer function is equivalent to a advanced controller.The time constant of the zero  is 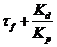.The time constant of pole (filter) is .It can be seen clearly that zero is slower than the pole. Select the controller zero that is on the right of the first stable pole in the system, here takes it -10.The time constant of the filter is 25 ms, the pole is -40. Transfer function of controller is:

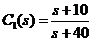
进而绘制出系统根轨迹.

Then mapped system root locus.

比例微分控制器影响系统的稳定性和暂态特性．而要改善系统的稳态特性可以采用PI(比例积分)控制

系统．PI控制器传递函数为：

PD controller influence stability and transient characteristics of the system. But to improve the steady state performance of the system, PI (proportional integral) control system can be used. Transfer function of the PI controller:

其有一个极点在原点处，一个零点在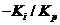处．如果和系统其他零极点相比，Pl控制器的零点与极点相距很近，则当PI控制器和PD控制器串联时，它对系统暂态特性的影响可以忽略．本控制系统中选择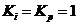.用MATLAB仿真采用PID控制器的磁悬浮模型闭环系统脉冲响应．

Where there is a pole at the origin, A zero at the 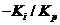. If contrary to the oter pole-zero of the system 其他, zeros and poles of the Pl controller is in close location. When the PI controller and the PD controller are in series, the influence it caused to the transient performance of the system can be ignored.In this control system,we select .

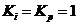Do MATLAB simulation for the closed-loop system of the magnetic levitation model (using PID controller)to acquire impulse response.

Simulation results are as follows:

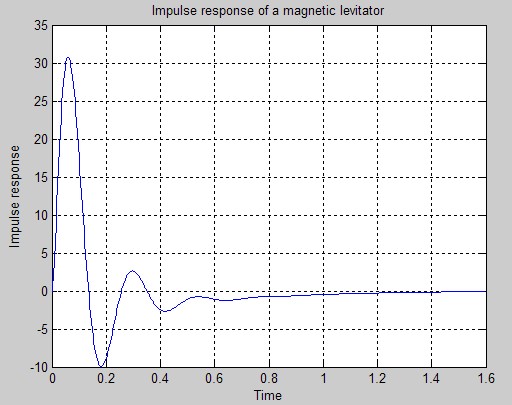
由仿真结果可见磁悬浮模型受到脉冲干扰会离开平衡位置，干扰消除后，在平衡位置上下减幅振动几次后可以回到原来位置，即系统是稳定的；系统自动调节速度较快，稳态误差较小．结果表明控制器是有效的．

It can be seen by the the simulation results that magnetic levitation model will leave the equilibrium position by pulse interference. After the interference cancellation, it can return to its original position after a few times of the upper and lower reducted vibration in the equilibrium position.So the system is stable. The system automatically adjust speed faster, steady-state error smaller. The results show that the controller is effective.

The simulation schematic of PID controller

摘要：

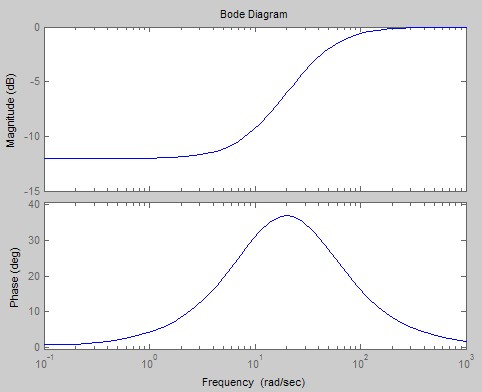
本文通过建立磁悬浮控制系统的数学模型，设计了磁悬浮PID控制器，并对系统应用MATLAB仿真，绘制了其根轨迹曲线和伯德图，进而分析了系统稳定性。根据传递函数搭建了simulink的仿真模型，在示波器观察阶跃响应波形，适当调整PID参数，使系统动态性能达到良好。

The paper establishes the mathematical model of maglev control system in which PID controller is designed for.And do the MATLAB simulation of the system, drawing its root locus curve and Bode diagram.Then analyzes the system stability. Simulation model is built based on  the transfer function.Observe the step response waveform in the oscilloscope. Adjusting the PID parameters appropriately  to achieve good dynamic performance of the system.

 maglev  MATLAB   stability  simulink

免责声明/版权申明 Passiontech

    所有文章为网上搜集或私下交流学习之用，任何涉及商业盈利目的均不得使用，否则产生的一切后果由您自己承担!

    本站仅仅提供一个观摩学习的环境，将不对任何资源负法律责任。所有资源请在下载后24小时内删除。

    若无意中侵犯到您的版权利益，请来信联系我们，我们会在收到信息三天内给予处理!

参数资料:

基于MATLAB的磁悬浮控制系统的研究MATLAB,磁悬浮控制系统,研究