жСШи¶БпЉЪ
иЃЊиЃ°ж†ЗеЗЖеТМеРДз±їеЗЇи°МпЉМзОѓеҐГеПКз§ЊдЉЪзЪДеПСе±ХйҐДжµЛпЉМеѓєеЕ≠иљ¶йБУзЪДж°•йЭҐзЪДзЪДдЇ§йАЪжµБињЫи°МйҐДжµЛж®°жЛЯпЉМеєґеЃЮзО∞еЕґеПѓиІЖеМЦпЉМзЫіиІВеЬ∞дЇЖиІ£жЬ™жЭ•ж°•йЭҐзЪДиљ¶жµБж®°еЉПпЉМдЄЇиѓДдЉ∞еТМдњЃж≠£иЃЊиЃ°жЦєж°ИжПРдЊЫдЊЭжНЃгАВ
жЬђдљЬеУБеИ©зФ®MATLABиљѓдїґжЦєдЊњзЪДжКАжЬѓжЦєж≥ХжЭ•еЃЮзО∞дЇ§йАЪжµБзЪДж®°жЛЯеТМеПѓиІЖеМЦпЉМеЕЈжЬЙиЊГеЉЇзЪДеПѓиѓїжАІеТМеПѓжОІеИґжАІгАВ
1 еЉХи®А
иЃ°зЃЧжЬЇж®°жЛЯжКАжЬѓдљЬдЄЇдЄАйЧ®зЛђзЂЛзЪДе≠¶зІСеІЛдЇО20дЄЦзЇ™40еєідї£гАВ70еєідї£дї•жЭ•пЉМйЪПзЭАз≥їзїЯзІСе≠¶дЄОиЃ°зЃЧжЬЇзІСе≠¶жКАжЬѓзЪДеПСе±ХпЉМж®°жЛЯжКАжЬѓеЊЧеИ∞дЇЖињЕзМЫзЪДеПСе±ХпЉМеЈ≤зїПеєњж≥ЫеЬ∞еЇФзФ®еЗ†дєОжЙАжЬЙзЪДе≠¶зІСгАВеЬ®дЇ§йАЪињРиЊУз≥їзїЯзЪДиІДеИТгАБиЃЊиЃ°гАБињРиР•еИЖжЮРз≠ЙжЦєйЭҐзЪДеЇФзФ®жЫіжШѓеЊЧеИ∞дЇЖйХњиґ≥еПСе±ХпЉМеєґеЬ®дЇ§йАЪињРиЊУеЈ•з®Ле≠¶зІСдЄ≠嚥жИРдЇЖдЇ§йАЪж®°жЛЯињЩдЄАеі≠жЦ∞зЪДйҐЖеЯЯгАВ
дЇ§йАЪж®°жЛЯжКАжЬѓеЬ®еИЖжЮРгАБиѓДдїЈеЕђиЈѓињРиЊУз≥їзїЯеПКеЕґжЮДжИРеНХеЕГдЄ≠иµЈдЄїи¶БиІТиЙ≤гАВеЃГдїђйАЪеЄЄдЄОеЕґдїЦиѓЄе¶ВдЊЫзїЩ-йЬАж±ВеИЖжЮРгАБйАЪи°МиГљеКЫеИЖжЮРгАБдЇ§йАЪжµБж®°жЛЯгАБиЈЯиљ¶зРЖиЃЇгАБж≥ҐеК®зРЖиЃЇз≠ЙеИЖжЮРжЦєж≥ХзЫЄзїУеРИжЭ•жЮДйА†е§НжЭВзЪДеЕђиЈѓдЇ§йАЪе≠Рз≥їзїЯпЉМжИЦдЄАдЇЫе≠Рз≥їзїЯзїПињЗзЫЄдЇТдљЬзФ®иАМзїДжИРзЪДе§Із≥їзїЯзЪДж®°жЛЯж°ЖжЮґгАВињЩдЇЫе≠Рз≥їзїЯеПѓдї•жШѓеНХдЄ™зЪДдњ°еПЈдЇ§еПЙеП£гАБжЧ†дњ°еПЈдЇ§еПЙеП£гАБе±Еж∞СеМЇжИЦеХЖдЄЪдЄ≠ењГеМЇзЪДдЇ§йАЪеѓЖйЫЖиЈѓзљСгАБзЇњжОІжИЦзљСжОІдњ°еПЈз≥їзїЯгАБйЂШйАЯеЕђиЈѓгАБдє°жЭСеПМиљ¶йБУеЕђиЈѓжИЦе§Ъиљ¶йБУеЕђиЈѓз≥їзїЯгАВ
еИ∞зО∞еЬ®дЄЇж≠ҐпЉМеПѓдї•иѓідЇ§йАЪйЧЃйҐШзЪДз†Фз©ґеЈ≤зїПжЬЙдЄЙзІНжЦєж≥Х——зїПй™МеЃЮжµЛжЦєж≥ХгАБзРЖиЃЇеИЖжЮРжЦєж≥ХгАБиЃ°зЃЧжЬЇж®°жЛЯжЦєж≥ХгАВжЬАеЄЄзФ®зЪДжЦєж≥ХжШѓзїПй™МеЃЮжµЛж≥ХгАВеЃЮжµЛж≥ХзЪДжЬАе§ІдЉШзВєжШѓеЯЇжЬђжХ∞жНЃйГљжЭ•жЇРдЇОеЃЮйЩЕзО∞еЬЇпЉМжЬЙйЩРе§ІзЪДеПѓдњ°еЇ¶пЉМдЄНйЬАи¶БдїАдєИеБЗиЃЊжЭ°дїґгАВдљЖжШѓпЉМеЕґеЉ±зВєжШѓеѓєдЇОдЄ™еИЂеЫ†зі†зЪДељ±еУНжГЕеЖµеЊИйЪЊз°ЃеЃЪгАВзРЖиЃЇеИЖжЮРж≥ХпЉМжАїжШѓи¶БйЗЗеПЦдЄАдЇЫеЯЇжЬђеБЗиЃЊпЉМињЩдЇЫеБЗиЃЊеПЧзРЖиЃЇз†Фз©ґиАЕж∞іеє≥зЪДйЩРеИґжЬЙдЇЫеПѓиГљдЄНж≠£з°ЃпЉМењЕеЃЪжИЦе§ЪжИЦе∞СеЬ∞дЄОеЃЮйЩЕжЬЙдЇЫеБПеЈЃгАВеЕґдЉШзВєжШѓеѓєдЇОдЄ™еИЂеЫ†зі†зЪДељ±еУНжЬЙжШОз°ЃзЪДжХ∞йЗПеЕ≥з≥їи°®з§ЇгАВиЃ°зЃЧжЬЇж®°жЛЯеИЩйЧіжЬЙдї•дЄКдЄ§зІНжЦєж≥ХзЪДдЉШзВєпЉМзФ±дЇОиЃ°зЃЧжЬЇж®°жЛЯж®°еЮЛжШѓзРЖиЃЇжО®жЉФпЉМжКљи±°еЗЇжЭ•зЪДпЉМиАМдЄАдЇЫеЯЇжЬђжХ∞жНЃеИЩжШѓжЭ•иЗ™зО∞еЬЇеЃЮжµЛпЉМиАМдЄФеИ©зФ®иЃ°зЃЧжЬЇж®°жЛЯжЦєж≥ХиГљдЇІзФЯеЊИе§ЪеГПеЃЮжµЛж≥ХйВ£ж†ЈеЊЧеИ∞зЪДдЇ§йАЪжХ∞жНЃгАВ
MATLAB жШѓдЄАзІНзФ®дЇОзЃЧж≥ХеЉАеПСгАБжХ∞жНЃеПѓиІЖеМЦгАБжХ∞жНЃеИЖжЮРдї•еПКжХ∞еАЉиЃ°зЃЧзЪДйЂШзЇІжКАжЬѓиЃ°зЃЧиѓ≠и®АеТМдЇ§дЇТеЉПзОѓеҐГпЉМжЛ•жЬЙеПЛе•љзЪДеЈ•дљЬеє≥еП∞еТМзЉЦз®ЛзОѓеҐГпЉМзЃАеНХжШУзФ®зЪДз®ЛеЇПиѓ≠и®АпЉМеЉЇе§ІзЪДзІСе≠¶иЃ°зЃЧжЬЇжХ∞жНЃе§ДзРЖиГљеКЫпЉМеЗЇиЙ≤зЪДеی嚥е§ДзРЖеКЯиГљпЉМеЇФзФ®еєњж≥ЫзЪДж®°еЭЧйЫЖеРИеЈ•еЕЈзЃ±пЉМеЃЮзФ®зЪДз®ЛеЇПжО•еП£еТМеПСеЄГеє≥еП∞з≠ЙиѓЄе§ЪдЉШзВєпЉМжЦєдЊњдЇ§йАЪжµБж®°жЛЯзЪДеЃЮзО∞еТМеПѓиІЖеМЦпЉМе§Іе§ІеЗПиљїз®ЛеЇПиѓ≠и®АзЪДе§НжЭВз®ЛеЇ¶гАВ
2 еЕ≠иљ¶йБУдЇ§йАЪжµБзЪДињРи°Мж®°еЮЛ
еїЇзЂЛдЇ§йАЪжµБж®°еЮЛзЪДж†єжЬђзЫЃзЪДжШѓи¶Бдї•иґ≥е§ЯзЪДз≤ЊеЇ¶жЭ•еЖНзО∞еЃҐиІВзЪДдЇ§йАЪзО∞и±°пЉМеЬ®ињЫи°МдЇ§йАЪжµБзЪДеЊЃиІВж®°жЛЯзЪДињЗз®ЛдЄ≠пЉМж†єжНЃдЇ§йАЪжµБеИЖеЄГзЪДдЄАиИђиІДеЊЛгАБдЇ§йАЪи∞ГжЯ•еТМеЯЇжЬђзїПй™МдЄЇеЯЇз°АпЉМеЕ®йЭҐжЮДйА†иљ¶иЊЖзЪДеИ∞иЊЊпЉМиљ¶жµБеИЖеЄГпЉМиљ¶иЊЖз±їеЮЛпЉМиљ¶йАЯпЉМеЬ®иЈѓжЃµдЄКиЗ™зФ±и°Мй©ґпЉМиЈЯй©∞з≠ЙгАВињЩйЗМзЪДдЇ§йАЪж®°еЮЛдЄїи¶БеМЕжЛђдЄ§йГ®еИЖпЉЪдЄАжШѓиљ¶иЊЖзЪДдЇІзФЯж®°еЮЛпЉЫдЇМжШѓиљ¶иЊЖзЪДи°Мй©ґж®°еЮЛгАВ
иљ¶иЊЖдЇІзФЯж®°еЮЛе∞±жШѓиљ¶иЊЖзЪДиЊУеЕ•йГ®еИЖпЉМдљЬзФ®дЄО襀殰жЛЯиЈѓжЃµзЪДиµЈеІЛжЦ≠йЭҐдЄКпЉМеЃГдЊЭдЊЭйЭ†йЪПжЬЇжКАжЬѓдЇІзФЯзђ¶еРИзїЩеЃЪеПВжХ∞зЪДж≥КжЭЊеИЖеЄГпЉМеРСз≥їзїЯжПРдЊЫеИЭеАЉпЉМеєґдї•зїПй™Мж¶ВзОЗеИЖеЄГдЇОеЕ≠дЄ™дЄНеРМзЪДиљ¶йБУгАВиљ¶иЊЖзЪДи°Мй©ґж®°еЮЛеН≥жШѓеПНеЇФиљ¶иЊЖеЬ®иЈѓжЃµдЄКи°Мй©ґзКґжАБеПШеМЦзЪДж®°еЮЛпЉМжЬђжЦЗж†єжНЃдЇ§йАЪи∞ГжЯ•еЊЧеЗЇзЪДдЄАиИђиљ¶жµБиљ¶иЊЖз±їеЮЛзЪДеИЖеЄГе∞Жиљ¶иЊЖеИЖдЄЇеНБдЄАзІНз±їеЮЛпЉМеЙНеЕ≠зІНдЄЇеЫЇеЃЪиљ¶йЗНзЪДиљ¶иЊЖпЉМдї•еРДиЗ™дЄНз≠ЙзЪДж¶ВзОЗеЗЇзО∞еЬ®ж®°жЛЯиЈѓжЃµзЪДиљ¶йБУдЄКпЉЫеРОеЕ≠зІНиљ¶жШѓеПШиљљзЪДиљ¶иЊЖпЉМе∞ЖеЕґеИЖдЄЇз©Їиљ¶еТМжї°иљљдЄ§зІНжГЕеЖµпЉИдЄНиЃ°иљ¶иЊЖеНКиљљжГЕеЖµпЉЙпЉМеєґдї•дЄНеРМзЪДж¶ВзОЗеЗЇзО∞гАВиљ¶йАЯж†єжНЃдЇ§йАЪи∞ГжЯ•жЙАеЊЧзЪДеРДз±їеЮЛзЪДиљ¶иЊЖзЪДеє≥еЭЗиљ¶йАЯпЉМеєґеЕБиЃЄеЕґйЪПжЬЇдЇІзФЯдЄКдЄЛжХ∞еАЉдЄЇμзЪДйЬЗиН°пЉМињЩйЗМжИСдїђеПЦμдЄЇ0.1гАВ
2.1 ж®°жЛЯеЯЇжЬђеПВжХ∞з°ЃеЃЪ
ж°•йЭҐйХњеЇ¶пЉИз±≥пЉЙ---------bridgeLength=1080*2=2160пЉЫ
ж°•йЭҐеЃљеЇ¶пЉИз±≥пЉЙ---------bridgeWidth=33пЉЫ
ж®°жЛЯжАїжЧґйЧіпЉИзІТпЉЙ-------T=3*7*24*60*60s
еЯЇеЗЖж±љиљ¶йХњеЇ¶пЉИз±≥пЉЙ-----vehicleLength=2.5;
еЯЇеЗЖж±љиљ¶еЃљеЇ¶пЉИз±≥пЉЙ-----vehicleWidth=1.8;
иљ¶йБУеЃљеЇ¶пЉИз±≥пЉЙ---------laneWidth=3.75;
иљ¶йБУжХ∞йЗП---------------laneNumber=6;
жЧґйЧіж≠•йХњпЉИзІТпЉЙ---------dt=1s
еРДиљ¶еЮЛеє≥еЭЗиљ¶йАЯ (m/s) пЉЪ
vave(1)=91.38/3.6; vave(2)=77.08/3.6;
vave(3)=77.08/3.6; vave(4)=74.34/3.6;
vave(5)=74.34/3.6; vave(6)=63.06/3.6;
vave(7)=63.06/3.6; vave(8)=63.39/3.6;
vave(9)=51.49/3.6; vave(10)=53.98/3.6;
vave(11)=43.31/3.6;
2.2 иљ¶иЊЖзЪДйЪПжЬЇдЇІзФЯ
жЬђжЦЗзЪДйЪПжЬЇиљ¶иЊЖдЇІзФЯжШѓдЊЭжНЃж≥КжЭЊеИЖеЄГеОЯзРЖзЪДжЦ≠йЭҐеПСиљ¶ж®°еЮЛгАВиљ¶иЊЖињЫеЕ•ж®°жЛЯиЈѓжЃµжШѓдЄ™йЪПжЬЇжАІдЇЛдїґпЉМеЫ†ж≠§пЉМеПѓе∞ЖеЕґиљђеМЦдЄЇињЫеЕ•ж®°жЛЯиЈѓжЃµзЪДиљ¶иЊЖдєЛйЧізЪДйЧійЪФжЧґйЧіиІЖдЄЇйЪПжЬЇйЗПгАВж†єжНЃиљ¶иЊЖињЫеЕ•ж®°жЛЯиЈѓжЃµжЬђиЇЂзЪДзЙєзВєпЉМдїОзРЖиЃЇдЄКеЇФжї°иґ≥дЄЛеИЧжЭ°дїґпЉЪ
1)еЬ®дЄНзЫЄйЗНеП†зЪДжЧґйЧіеМЇйЧіеЖЕиљ¶иЊЖзЪДдЇІзФЯжШѓдЇТзЫЄзЛђзЂЛзЪДпЉМеН≥жЧ†еРОжХИжАІпЉЫ
2)еѓєеЕЕеИЖе∞ПзЪД tпЉМеЬ®жЧґйЧЃеМЇйЧі[tпЉМt+ t]еЖЕжЬЙдЄАиЊЖиљ¶дЇІзФЯзЪДж¶ВзОЗдЄОtжЧ†еЕ≥пЉМиАМдЄОеМЇйЧійХњеЇ¶ tжИРж≠£жѓФпЉМеН≥иљ¶иЊЖзЪДдЇІзФЯеЕЈжЬЙеє≥з®≥жАІпЉЫ
3)еѓєдЇОеЕЕеИЖе∞ПзЪД tпЉМеЬ®жЧґйЧіеМЇйЧі[tпЉМt+ t]еЖЕдЄАжЭ°иљ¶йБУдЄКжЬЙ2иЊЖжИЦ2иЊЖдї•дЄКиљ¶иЊЖдЇІзФЯзЪДж¶ВзОЗжЮБе∞ПпЉМеН≥еЕЈжЬЙжЩЃйБНжАІгАВ
P(k)=
еЕґдЄ≠: PпЉИkпЉЙ---и°®з§ЇеЬ®иЃ°жХ∞йЧійЪФtеЖЕеИ∞иЊЊkиЊЖиљ¶жИЦkдЄ™дЇЇзЪДж¶ВзОЗпЉЫ
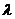 --------и°®з§ЇеНХдљНжЧґйЧійЧійЪФзЪДеє≥еЭЗеИ∞иЊЊзОЗпЉИиЊЖ/sжИЦдЇЇ/sпЉЙпЉЫ
--------и°®з§ЇеНХдљНжЧґйЧійЧійЪФзЪДеє≥еЭЗеИ∞иЊЊзОЗпЉИиЊЖ/sжИЦдЇЇ/sпЉЙпЉЫ
t--------дЄЇжѓПдЄ™иЃ°жХ∞йЧійЪФжМБзї≠зЪДжЧґйЧіжИЦиЈЭз¶їгАВ
жЦЗдЄ≠еЇФзФ®MATLABдЄ≠еЈ•еЕЈеЗљжХ∞poissrndпЉИпЉЙдЇІзФЯдЄАзїДйЪПжЬЇжХ∞пЉМжЬЙжХИеЬ∞жППињ∞дЇЖиљ¶иЊЖеЬ®дЄ™иљ¶йБУдЇІзФЯзЪДж¶ВзОЗгАВ
дї•дЄЛдЄЇйАЪињЗmatlabдЇІзФЯжЦ∞иљ¶жµБзЪДдї£з†БпЉИдї•зђђдЄАз±їиљ¶иЊЖдЄЇдЊЛпЉМеП™еИЧеЗЇе±АйГ®пЉЙпЉЫ
| |
| |
%--------create new vehicle-------------
sn=poissrnd(2*flux*deltat/3600);
for m=1:sn
%-----------------------
typernd=unifrnd(0,1);
if typernd<=0.4822
type=1;
lanernd=unifrnd(0,1);
if lanernd<=0.5068
laneArr=[3,4];
lanenum=laneArr(ceil(unifrnd(0,2)));
elseif lanernd>0.5068 & lanernd<=0.8546
laneArr=[2,5];
lanenum=laneArr(ceil(unifrnd(0,2)));
else
laneArr=[1,6];
lanenum=laneArr(ceil(unifrnd(0,2)));
end
……
end
|
|
иљ¶жµБеЬ®дЄ™иљ¶йБУзЪДеИЖйЕН
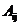 зђђ
зђђ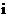 з±їиљ¶еЬ®зђђ
з±їиљ¶еЬ®зђђ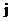 иљ¶йБУеЗЇзО∞зЪДж¶ВзОЗ
иљ¶йБУеЗЇзО∞зЪДж¶ВзОЗ

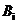 и°®з§ЇйЪПжЬЇдЇІзФЯзЪДиљ¶жµБдЄ≠
и°®з§ЇйЪПжЬЇдЇІзФЯзЪДиљ¶жµБдЄ≠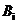 зђђ
зђђ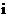 з±їиљ¶еЗЇзО∞зЪДж¶ВзОЗ
з±їиљ¶еЗЇзО∞зЪДж¶ВзОЗ
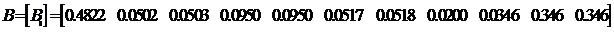
иљ¶йАЯзЪДз°ЃеЃЪ
жЬђж®°еЮЛдЄ≠зЪДиљ¶йАЯжХ∞жНЃжЭ•иЗ™дЇ§йАЪи∞ГжЯ•жЙАеЊЧзЪДеє≥еЭЗиљ¶йАЯпЉМдї•m/sиЃ°пЉМзФ®vave(i)=Vi/3.6жЭ•иљђеМЦпЉМiи°®з§Їиљ¶иЊЖз±їеЮЛпЉМViдЄЇдЇ§йАЪи∞ГжЯ•жЙАеЊЧиљ¶йАЯгАВдЄЇдЇЖжЫіеК†зЬЯеЃЮеЬ∞ж®°жЛЯдЇ§йАЪжµБзЪДиљ¶йАЯпЉМжИСдїђеЕБиЃЄиљ¶йАЯеЬ®дЄАеЃЪиМГеЫіеЖЕйЬЗиН°пЉМеПЦйЬЗиН°з≥їжХ∞μ=0.1
еН≥пЉЪ vave(VT)*(1+unifrnd(-0.1,0.1)
иљ¶йХњзЪДз°ЃеЃЪ
дї•иљ¶иЊЖз±їеЮЛ1зЪДиљ¶йХњдЄЇеЯЇеЗЖиљ¶йХњпЉМиљ¶еЃљпЉМиљ¶йХњдЄЇ2.5mпЉМиљ¶еЃљ1.8mпЉМеЕґдїЦеРДзІНз±їеЮЛзЪДиљ¶йХњзФ®еЯЇеЗЖиљ¶йХњдєШдї•дЄАдЄ™еРДиЗ™зЪДз≥їжХ∞пЉМеЊЧеЗЇеРДзІНиљ¶еЮЛзЪДе∞ЇеѓЄгАВ
еН≥пЉЪKпЉИiпЉЙ= C*KпЉИ1пЉЙ
C=Ci=[1пЉМ1.32пЉМ1.88пЉМ2.4пЉМ1.32пЉМ1.6пЉМ2.2пЉМ3.4пЉМ4.8пЉМ5.4пЉМ5.2]
иљ¶йЗНзЪДз°ЃеЃЪ
ж†єжНЃдЇ§йАЪи∞ГжЯ•зїУжЮЬеТМзРЖиЃЇеИЖжЮРпЉМеЙНеЕ≠зІНиљ¶еЮЛдЄЇжБТеЃЪиљ¶йЗНиљ¶еЮЛпЉМиљ¶йЗНжЬНдїОдЄАеЃЪеПВжХ∞зЪДж≠£жАБеИЖеЄГпЉМеРОдЇФзІНиљ¶еЮЛдЄЇеПШиљ¶йЗНиљ¶еЮЛпЉМз©Їиљ¶еТМиљљйЗНеИЖеИЂдї•дЄНеРМзЪДж¶ВзОЗеЗЇзО∞гАВ
еН≥пЉЪ


2.3 иљ¶жµБињРи°МзЪДеК®жАБж®°жЛЯ
ињРзФ®matlabзЪДзїШеЫЊеКЯиГљеЃЮзО∞дЇ§йАЪжµБзЪДеПѓиІЖеМЦеК®жАБж®°жЛЯпЉИз®ЛеЇПе¶ВйЩДељХпЉЙгАВ
ињРи°МзїУжЮЬе¶ВдЄЛпЉЪињРи°МеИЭпЉИе¶ВеЫЊдЄАпЉЙпЉМињРи°МдЄ≠пЉИе¶ВеЫЊдЇМпЉЙпЉМињРи°МеЃМжѓХпЉИе¶ВеЫЊдЄЙпЉЙгАВ
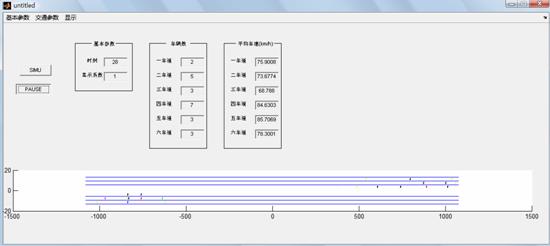
еЫЊдЄА
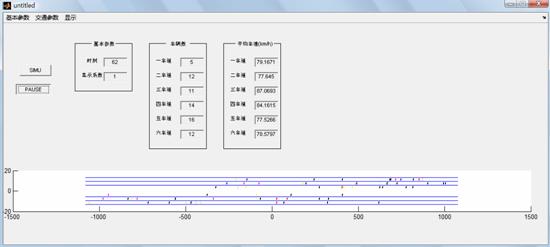
еЫЊдЇМ
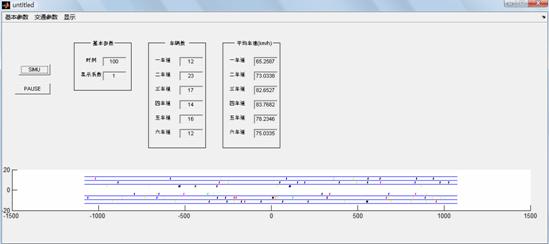
еЫЊдЄЙ
2.4 ж®°жЛЯзїУжЮЬеТМиЃ®иЃЇ
йАЪињЗиѓ•ж®°жЛЯзЪДињРи°МпЉМеПѓдї•зЫіиІВеЬ∞зЬЛеЗЇеЬ®жЙАиЃЊзљЃзЪДжЭ°дїґдЄЛзЪДдЇ§йАЪжµБеИЖеЄГеТМињРи°МжГЕеЖµпЉМзЫіиІВеЬ∞зЬЛеЗЇиЃЊиЃ°еПВжХ∞дЄЛзЪДеЃЮйЩЕињРи°МжХИжЮЬпЉМдЄЇжФєињЫиЃЊиЃ°еТМеПВжХ∞жПРдЊЫдЊЭжНЃпЉМиЊЊеИ∞ењЂйАЯпЉМеЃЙеЕ®гАВйЂШжХИзЪДеЃЮй™МжХИжЮЬгАВ
дљЖжШѓжЬђдљЬеУБињШе≠ШеЬ®зЭАдЄАеЃЪзЪДдЄНиґ≥пЉМе¶ВжЬЙдЇЫеПВжХ∞жШѓзЙєеЃЪиЃЊиЃ°зЪДпЉМиЈЯе§ЪеПШеЃЮйЩЕжГЕеЖµдЉЪжЬЙдЄАеЃЪзЪДеЗЇеЕ•пЉМеЬ®иљ¶жµБеТМиљ¶йАЯзЪДж®°жЛЯдЄ≠дєЯињЫи°МдЇЖдЄАеЃЪзЪДзРЖжГ≥жАІзЃАеМЦз≠ЙгАВ
еПВиАГжЦЗзМЃпЉЪ
[1]гАБеЃЗдїБеЊЈпЉМжЭОе§ІйЊЩ.еЯЇдЇОеЕГиГЮиЗ™еК®жЬЇзЪДдЇ§йАЪжµБиЃ°зЃЧжЬЇж®°жЛЯ.иЃ°зЃЧжЬЇдїњзЬЯ.зђђ25еНЈ.зђђ8жЬЯ.271-274;
[2]гАБзОЛзВЬпЉМињЗзІАжИР.дЇ§йАЪеЈ•з®Ле≠¶.еНЧдЇђпЉЪдЄЬеНЧе§Іе≠¶еЗЇзЙИз§ЊпЉМ2000.9пЉЫ
[3]гАБзљЧеїЇеЖЫпЉМжЭ®зР¶.з≤ЊиЃ≤е§ЪзїГMATLAB.—и•њеЃЙ.и•њеЃЙдЇ§йАЪе§Іе≠¶еЗЇзЙИз§ЊпЉМ2002.8пЉЫ
[4]гАБеС®еХЖеРЊз≠Й.дЇ§йАЪеЈ•з®Л.—дЄКжµЈпЉМеРМжµОе§Іе≠¶еЗЇзЙИз§ЊпЉМ1987.10пЉЫ
[5]гАБйЭ≥жЦЗиИЯпЉМеЉ†жЭ∞пЉМжҐЕеЖђиК≥.еЯЇдЇОзїЖиГЮиЗ™еК®жЬЇж®°еЮЛзЪДдЇ§йАЪжµБж®°жЛЯз®ЛеЇП.еНОеНЧзРЖеЈ•е§Іе≠¶е≠¶жК•пЉИиЗ™зДґзІСе≠¶зЙИпЉЙ.зђђ35еНЈ зђђ5жЬЯ.34-38.
еЕНиі£е£∞жШО/зЙИжЭГзФ≥жШО Passiontech
жЙАжЬЙжЦЗзЂ†дЄЇзљСдЄКжРЬйЫЖжИЦзІБдЄЛдЇ§жµБе≠¶дє†дєЛзФ®пЉМдїїдљХжґЙеПКеХЖдЄЪзЫИеИ©зЫЃзЪДеЭЗдЄНеЊЧдљњзФ®пЉМеР¶еИЩдЇІзФЯзЪДдЄАеИЗеРОжЮЬзФ±жВ®иЗ™еЈ±жЙњжЛЕ!
жЬђзЂЩдїЕдїЕжПРдЊЫдЄАдЄ™иІВжС©е≠¶дє†зЪДзОѓеҐГпЉМе∞ЖдЄНеѓєдїїдљХиµДжЇРиіЯж≥ХеЊЛиі£дїїгАВжЙАжЬЙиµДжЇРиѓЈеЬ®дЄЛиљљеРО24е∞ПжЧґеЖЕеИ†йЩ§гАВ
иЛ•жЧ†жДПдЄ≠дЊµзКѓеИ∞жВ®зЪДзЙИжЭГеИ©зЫКпЉМиѓЈжЭ•дњ°иБФз≥їжИСдїђпЉМжИСдїђдЉЪеЬ®жФґеИ∞дњ°жБѓдЄЙ姩еЖЕзїЩдЇИе§ДзРЖ!
 жФґиЧПиС©жШЯ
жФґиЧПиС©жШЯ










 400-878-1895
400-878-1895 px51870017
px51870017
















